题目内容
9.如图甲所示,质量m=1kg的小物体放在长直的水平地面上,用水平细线绕在半径R=0.2m的、质量M=1kg的薄圆筒上.t=0时刻,圆筒在电动机的带动下由静止开始绕竖直的中心轴转动,小物体的v-t图象如图乙所示,小物体和地面间的动摩擦因数μ=0.2,则( )
| A. | 圆筒转动的角速度随时间的变化关系满足ω=4t | |
| B. | 细线的拉力大小为2N | |
| C. | 细线拉力的瞬时功率满足P=4t | |
| D. | 在0-2s内,电动机做的功为8J |
分析 根据图象得出物体物体速度随时间变化的关系式,圆筒边缘线速度与物块前进速度大小相同,根据v=ωR求出角速度随时间的变化关系,根据图象求出加速度,再根据牛顿第二定律求出拉力,根据P=Fv求解细线拉力的瞬时功率,根据能量守恒求出在0-2s内,电动机做的功.
解答 解:A、根据图象可知,小物体做匀加速直线运动,速度随时间变化的关系式为v=t,圆筒边缘线速度与物块前进速度大小相同,
根据v=ωR得:ω=5t,故A错误;
B、物体运动的加速度a=$\frac{△v}{△t}=\frac{2}{2}=1m/{s}^{2}$,根据牛顿第二定律得:
F-μmg=ma
解得:F=1×1+0.2×10=3N,故B错误;
C、细线拉力的瞬时功率P=Fv=3t,故C错误;
D、物体在2s内运动的位移x=$\frac{1}{2}×2×2=2m$,
根据能量守恒可知,电动机做的功转化为物体和圆筒的动能以及克服摩擦力做的功,则有:
W=$\frac{1}{2}(M+m){{v}_{2}}^{2}$+fx=$\frac{1}{2}×(1+1)×{2}^{2}+0.2×10×2=8J$,故D正确.
故选:D
点评 本题考查牛顿第二定律、速度时间图象的性质、圆的性质等内容,要求能正确理解题意,并分析物体的爱力情况及能量转化过程,难度适中.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.地球的质量和半径分别是火星的10倍和2倍,地球表面的重力加速度为g,则火星表面的重力加速度为( )
| A. | 0.2g | B. | 0.4g | C. | 2.5g | D. | 5g |
20. 如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
 如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )| A. | 电源1和电源2的内阻之比是7:5 | |
| B. | 在这两种连接状态下,小灯泡的电阻之比是16:21 | |
| C. | 在这两种连接状态下,电源的输出功率之比是3:2 | |
| D. | 在这两种连接状态下,电源的输出功率之比是7:12 |
17.用材料和粗细相同、长短不同的两段绳子,各拴一个质量相同的小球在光滑水平面上做匀速圆周运动,那么以下说法错误的是( )
| A. | 两个球以相同的线速度运动时,短绳易断 | |
| B. | 两个球以相同的角速度运动时,长绳易断 | |
| C. | 两个球以相同的周期运动时,长绳易断 | |
| D. | 两个小球以相同大小的加速度运动时,短绳易断. |
14.一物体做匀变速直线运动,下列说法中正确的是( )
| A. | 物体的末速度一定与时间成正比 | |
| B. | 物体的位移一定与时间的平方成正比 | |
| C. | 物体的速度在一定时间内发生的变化与这段时间成正比 | |
| D. | 若物体做匀加速直线运动,则速度和位移都随时间增大;若物体做匀减速直线运动,则速度和位移都随时间减小 |
1.关于下列四幅图片的描述正确的是( )
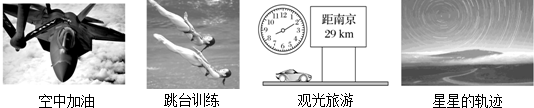

| A. | 认为加油机是运动的,选择的参考系是加油机中的飞行员 | |
| B. | 为了研究运动员的技术动作,不能将运动员视为质点 | |
| C. | 8点10分指的是时间,29 km指的是位移 | |
| D. | 天文爱好者经长时间曝光拍摄的“星星的轨迹”照片,这些有规律的弧线的形成,说明了太阳在运动 |
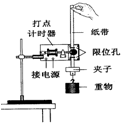 如图所示为用打点计时器验证机械能守恒定律的实验装置.
如图所示为用打点计时器验证机械能守恒定律的实验装置. 2009年在韩国江陵举办的世界冰壶锦标赛上,中国女子冰壶队在决赛中战胜冬奥会冠军瑞典女子冰壶队,第一次获得冰壶世界冠军.若运动员以一定的初速度将冰壶沿水平面推出,由于摩擦阻力的作用,其动能随位移变化图线如图所示,已知冰壶质量为20kg,g取10m/s2,则冰壶受到的阻力大小为16N,滑行时间等于10s.
2009年在韩国江陵举办的世界冰壶锦标赛上,中国女子冰壶队在决赛中战胜冬奥会冠军瑞典女子冰壶队,第一次获得冰壶世界冠军.若运动员以一定的初速度将冰壶沿水平面推出,由于摩擦阻力的作用,其动能随位移变化图线如图所示,已知冰壶质量为20kg,g取10m/s2,则冰壶受到的阻力大小为16N,滑行时间等于10s.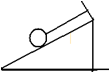 如图所示,一质量为0.2kg的小球用细绳吊在倾角为θ=53°的斜面上,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,求下列几种情况下,绳对球的拉力T的大小.
如图所示,一质量为0.2kg的小球用细绳吊在倾角为θ=53°的斜面上,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,求下列几种情况下,绳对球的拉力T的大小.