题目内容
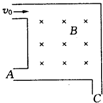 边长为a的正方形处于有界磁场中,如图所示.一束电子以速度v0水平射入磁场 后,分别从A处和C处射出,则vA:vC=
边长为a的正方形处于有界磁场中,如图所示.一束电子以速度v0水平射入磁场 后,分别从A处和C处射出,则vA:vC=1:2
1:2
,所经历的时间之比tA:tC=2:1
2:1
.分析:由几何关系可知从两孔射出的粒子的运动半径,则由洛仑兹力充当向心力可得出粒子的速度关系;由周期公式及转过的角度可求得时间之比;由向心力公式可求得加速度之比.
解答:解:电子从C点射出,A为圆心,Rc=L,圆心角θc=
由R=
,
得vc=
运动时间为四分之一周期,即:tc=
T=
电子从A点射出,OA中点为圆心,RA=
,圆心角θd=π,
所以vA=
,tA=tA=
T=
由于运动的周期与速度无关,是相等的,
故vA:vC=1:2,tA:C=2:1,
故答案为:1:2;2:1;
| π |
| 2 |
| mv |
| qB |
得vc=
| eBL |
| m |
| 1 |
| 4 |
| πm |
| 2eB |
电子从A点射出,OA中点为圆心,RA=
| L |
| 2 |
所以vA=
| eBL |
| 2m |
| 1 |
| 2 |
| πm |
| eB |
由于运动的周期与速度无关,是相等的,
故vA:vC=1:2,tA:C=2:1,
故答案为:1:2;2:1;
点评:本题为带电粒子在磁场中运动的基本问题,只需根据题意明确粒子的运动半径及圆心即可顺利求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
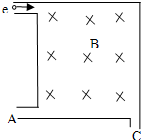 边长为a的正方形处于有界磁场中,如图所示.一束电子以水平速度射入磁场后,分别从A处和C处射出,则下列说法错误的是( )
边长为a的正方形处于有界磁场中,如图所示.一束电子以水平速度射入磁场后,分别从A处和C处射出,则下列说法错误的是( )

 边长为a的正方形处于有界磁场中,如图所示。一束电子以速度v0水平射入磁场后,分别从A处和C处射出,则VA:VC= ,所经历的时间之比tA:tB=
边长为a的正方形处于有界磁场中,如图所示。一束电子以速度v0水平射入磁场后,分别从A处和C处射出,则VA:VC= ,所经历的时间之比tA:tB=