��Ŀ����
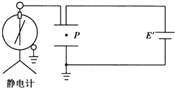
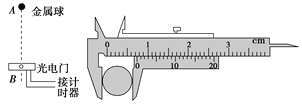
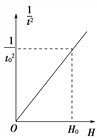
����Ŀ����ͼ��ʾ��A�ǵ����ͬ�����ǣ���һ����B��Բ�ι��λ�ڳ��ƽ���ڣ������߶�Ϊh.��֪����뾶ΪR��������ת���ٶ�Ϊ��0�� ���������������ٶ�Ϊg��OΪ�������ģ��� ��

A. �������ǵ�����ת������B����������Ϊ![]()
B. B���ǵ����ļ��ٶ�С�ڳ������������ļ��ٶ�
C. ����B���ǵ����ٶȴ���A���ǵ����ٶȣ�����B���Ǽ����п��ܵ���A�������ڹ��
D. ������B���з����������ת������ͬ��ijʱ��A��B������������(O��B��A��ͬһֱ����)�������پ��� ʱ�䣬������һ����������
ʱ�䣬������һ����������
���𰸡�AD
����������B���������������ṩ��������ʽ�ã�![]() ���Ե��������������������������ɵã�
���Ե��������������������������ɵã�![]() ��������ã�
��������ã�![]() ����A��ȷ������ţ�ٵڶ�����
����A��ȷ������ţ�ٵڶ�����![]() ����ã�
����ã�![]() ����֪B���ǵ����ļ��ٶȴ���ͬ���������ļ��ٶȣ�����a=��2r��ͬ���������ļ��ٶȴ��ڳ������������ļ��ٶȣ�����B���ǵ����ļ��ٶȴ��ڳ������������ļ��ٶȣ���B����B���Ǽ��٣��������˶��������ܵ���A�������ڹ������C����AB�ٴ�����ʱ��B��A��תһ�ܣ�
����֪B���ǵ����ļ��ٶȴ���ͬ���������ļ��ٶȣ�����a=��2r��ͬ���������ļ��ٶȴ��ڳ������������ļ��ٶȣ�����B���ǵ����ļ��ٶȴ��ڳ������������ļ��ٶȣ���B����B���Ǽ��٣��������˶��������ܵ���A�������ڹ������C����AB�ٴ�����ʱ��B��A��תһ�ܣ�![]() ���У�
����![]() ��
��![]() �������ɵã�
�������ɵã�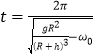 ����D��ȷ������AD��ȷ��BC����
����D��ȷ������AD��ȷ��BC����