题目内容
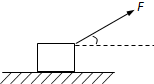 一个质量m=3kg的物体静止在水平桌面上,物体与桌面间的动摩擦因数为0.4,g取10m/s2,sin37°=0.6,cos37°=0.8.
一个质量m=3kg的物体静止在水平桌面上,物体与桌面间的动摩擦因数为0.4,g取10m/s2,sin37°=0.6,cos37°=0.8.(1)现给物体施加F=15N的水平力,求物体在2s内前进的位移?
(2)如图所示,物体受到与水平成37°角斜向上方的大小为15N的拉力作用,从静止开始运动2s内的位移为多少?
分析:(1)根据牛顿第二定律求出拉力F作用时的加速度,根据运动学位移公式求出2s内的位移.
(2)再根据牛顿第二定律求出物体的加速度,通过位移公式,求出物体的位移.
(2)再根据牛顿第二定律求出物体的加速度,通过位移公式,求出物体的位移.
解答:解:(1)当给物体施加F=15N的水平力,根据牛顿第二定律得:
F-f=ma1;
又f=μN=μmg
得:a1=
-μg=
-0.4×10=1m/s2
所以物体在2s内前进的位移为:x1=
a1t2=
×1×22m=2m.
(2)当物体受到与水平成37°角斜向上方的大小为15N的拉力作用,根据牛顿第二定律得:
竖直方向上:N′+Fin37°-mg=0…①
得:N′=mg-Fsin37°…②
水平方向上:Fcos37°-f′=ma2…③
又 f′μN′
所以:Fcos37°-μ(mg-Fsin37°)=ma2
解得:a2=
[Fcos37°-μ(mg-Fsin37°)]=
×[15×0.8-0.4×(30-15×0.6)]=1.2m/s2
从静止开始运动2s内的位移为:x2=
a2t2=
×1.2×22m=2.4m
答:(1)现给物体施加F=15N的水平力,物体在2s内前进的位移是2m.
(2)物体受到与水平成37°角斜向上方的大小为15N的拉力作用,从静止开始运动2s内的位移为2.4m.
F-f=ma1;
又f=μN=μmg
得:a1=
| F |
| m |
| 15 |
| 3 |
所以物体在2s内前进的位移为:x1=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当物体受到与水平成37°角斜向上方的大小为15N的拉力作用,根据牛顿第二定律得:
竖直方向上:N′+Fin37°-mg=0…①
得:N′=mg-Fsin37°…②
水平方向上:Fcos37°-f′=ma2…③
又 f′μN′
所以:Fcos37°-μ(mg-Fsin37°)=ma2
解得:a2=
| 1 |
| m |
| 1 |
| 3 |
从静止开始运动2s内的位移为:x2=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)现给物体施加F=15N的水平力,物体在2s内前进的位移是2m.
(2)物体受到与水平成37°角斜向上方的大小为15N的拉力作用,从静止开始运动2s内的位移为2.4m.
点评:本题综合考查了牛顿第二定律和运动学公式,知道加速度是联系力学和运动学的桥梁,在这类问题中加速度是必求的量.

练习册系列答案
相关题目
 (2012?湖南一模)如图所示,在高为h=5m的平台右边缘上,放着一个质量M=3kg的铁块,现有一质量为m=1kg的钢球以v0=10m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为l=2m.已知铁块与平台之间的动摩擦因数为0.5,求铁块在平台上滑行的距离s(不计空气阻力,铁块和钢球都看成质点).
(2012?湖南一模)如图所示,在高为h=5m的平台右边缘上,放着一个质量M=3kg的铁块,现有一质量为m=1kg的钢球以v0=10m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为l=2m.已知铁块与平台之间的动摩擦因数为0.5,求铁块在平台上滑行的距离s(不计空气阻力,铁块和钢球都看成质点).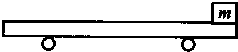 如图所示,质量M=10kg的小车放在光滑水平面上,在小车右端施加一水平恒力F=10N.当小车向右运动的速度达到4m/s时,在小车的右端轻轻放上一个质量m=3kg的小物块,小物块与小车的动摩擦因素μ=0.2,小物块始终不离开小车,求:
如图所示,质量M=10kg的小车放在光滑水平面上,在小车右端施加一水平恒力F=10N.当小车向右运动的速度达到4m/s时,在小车的右端轻轻放上一个质量m=3kg的小物块,小物块与小车的动摩擦因素μ=0.2,小物块始终不离开小车,求: (1)下列说法正确的是
(1)下列说法正确的是