题目内容
4. 如图,在竖直平面内有金属框ABCD,B=0.1T的匀强磁场垂直线框平面向外,线框电阻不计,框间距离为0.1m.线框上有一个长0.1m的可滑动的金属杆ab,已知金属杆质量为0.2g,金属杆电阻r=0.1Ω,电阻R=0.2Ω,不计其他阻力,求金属杆ab匀速下落时的速度.
如图,在竖直平面内有金属框ABCD,B=0.1T的匀强磁场垂直线框平面向外,线框电阻不计,框间距离为0.1m.线框上有一个长0.1m的可滑动的金属杆ab,已知金属杆质量为0.2g,金属杆电阻r=0.1Ω,电阻R=0.2Ω,不计其他阻力,求金属杆ab匀速下落时的速度.
分析 导体ab先向下做加速度逐渐减小的加速运动,当加速度减小到0,即安培力等于重力时,速度达到最大,达到稳定状态.根据平衡条件和安培力与速度的关系结合,即可求得最大速度.
解答 解:当ab棒匀速下落时速度最大且达到稳定状态,则有:
mg=ILB
又 感应电流,I=$\frac{E}{R+r}$,
且感应电动势,E=BLvm
联立三式得:vm=$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$=$\frac{0.2×1{0}^{-3}×10×(0.2+0.1)}{0.{1}^{2}×0.{1}^{2}}$m/s=6m/s
答:金属杆ab匀速下落时的速度6m/s.
点评 解决本题的关键能结合牛顿第二定律,正确分析出金属棒的运动情况,知道当加速度为0时,速度最大.并利用还可以求出安培力和平衡条件即为求解最大速度.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.关于平抛运动,下列说法错误的是( )
| A. | 平抛物体在运动过程中,其加速度和水平速度保持不变 | |
| B. | 平抛物体可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 | |
| C. | 平抛物体是做曲线运动的,因此它不可能是匀变速运动 | |
| D. | 平抛物体水平飞行的距离与初速度和高度有关有关 |
9.2015年3月30日,我国成功地发射了第17颗北斗导航卫星,距离最终建成具有我国独立自主知识产权的多功能北斗卫星导航系统又进了一步.该系统建成后将包括5颗同步轨道卫星和30颗一般轨道卫星,关于这些卫星正常绕地球运行时的说法,正确的是( )
| A. | 5颗同步卫星的轨道半径可以不同 | |
| B. | 5颗同步卫星的运行轨道必须在同一平面内,且与赤道面共面 | |
| C. | 导航系统中所有卫星的运行速度一定大于第一宇宙速度 | |
| D. | 导航系统中的不同卫星,运行轨道半径越大的,绕地运行的角速度也越大 |
16. 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )| A. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | B. | 人拉绳行走的速度为vcosθ | ||
| C. | 船的加速度为$\frac{Tcosθ-f}{m}$ | D. | 船的加速度为$\frac{T-f}{m}$ |
11.静电场中,以下说法正确的是( )
| A. | 由电场强度的定义式E=$\frac{F}{q}$ 可知电场强度E跟F成正比,跟q成反比 | |
| B. | 场的概念最早由法拉第提出,电场和电场线均不是客观存在的 | |
| C. | 电场中电势升高的方向一定是场强的反方向 | |
| D. | 电场中电场强度为零的地方电势不一定为零 |
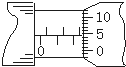 测一小球直径时,螺旋测微器的示数如图所示,可知该小球的直径为2.545mm,若将可动刻度顺时针转过72°(从右往左看),则读数为2.445mm.
测一小球直径时,螺旋测微器的示数如图所示,可知该小球的直径为2.545mm,若将可动刻度顺时针转过72°(从右往左看),则读数为2.445mm. 如图电路,开关原先闭合,电路处于稳定,在某一时刻突然断开开关S,则通过电阻R 1中的电流I1随时间变化的图线可能是下图中的( )
如图电路,开关原先闭合,电路处于稳定,在某一时刻突然断开开关S,则通过电阻R 1中的电流I1随时间变化的图线可能是下图中的( )



 如图是电熨斗温度自动控制装置.
如图是电熨斗温度自动控制装置.