题目内容
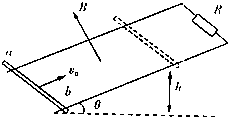 如图所示,一光滑平行金属轨道平面与水平面成θ角,两轨道上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆始终保持与导轨垂直且接触良好,且轨道与金属杆的电阻均忽略不计,则( )
如图所示,一光滑平行金属轨道平面与水平面成θ角,两轨道上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆始终保持与导轨垂直且接触良好,且轨道与金属杆的电阻均忽略不计,则( )| A、整个过程中金属杆所受合外力的冲量大小为2mv0 | ||||
B、上滑到最高点的过程中克服安培力与重力所做功之和等
| ||||
C、上滑到最高点的过程中克服R上产生的焦耳热等于
| ||||
| D、金属杆两次通过斜面上的同一位置时电阻R的热功率相同 |
分析:根据动量定理分析安培力的冲量.通过对导体棒受力分析知,上滑的过程做变减速直线运动,下滑的过程做变加速直线运动,抓住位移相等,比较安培力大小,即可分析克服安培力做功功率的大小,根据功能关系分析焦耳热的关系.在上滑过程中,导体棒减小的动能转化为重力势能和电阻R上产生的焦耳热,即可比较焦耳热与减少的动能的大小.
解答:解:A、在整个过程中,由于回路中产生内能,根据能量守恒定律得知,金属杆ab返回底端时速度v小于v0.取沿斜面向下为正方向,设合外力的冲量大小为I,根据动量定理得:I=mv-(-mv0)=mv+mv0<2mv0.故A错误.
B、上滑过程中,重力和安培力对杆做功,安培力做负功,根据动能定理得知:克服安培力与重力所做功之和等
m
.故B正确.
C、对于上滑过程,由动能定理得:-mgh-W安=0-
m
,得克服安培力做功为:W安=
m
-mgh.
根据功能关系可知,克服安培力做功等于回路中产生的焦耳热,即有Q=W安,则得:Q=
m
-mgh.故C正确.
D、上滑的过程做变减速直线运动,下滑的过程做变加速直线运动,经过同一位置时,上滑的速度大小大于下滑的速度大小,上滑的感应电动势大于下滑的感应电动势,上滑的感应电流大于下滑的感应电流,则上滑时所受的安培力大于下滑时的安培力,由P=Fv知,经过同一位置时,上滑过程中杆克服安培力做功的功率大于下滑过程,上滑过程中电阻R的热功率大于下滑过程R的热功率.故D错误.
故选:BC
B、上滑过程中,重力和安培力对杆做功,安培力做负功,根据动能定理得知:克服安培力与重力所做功之和等
| 1 |
| 2 |
| v | 2 0 |
C、对于上滑过程,由动能定理得:-mgh-W安=0-
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
根据功能关系可知,克服安培力做功等于回路中产生的焦耳热,即有Q=W安,则得:Q=
| 1 |
| 2 |
| v | 2 0 |
D、上滑的过程做变减速直线运动,下滑的过程做变加速直线运动,经过同一位置时,上滑的速度大小大于下滑的速度大小,上滑的感应电动势大于下滑的感应电动势,上滑的感应电流大于下滑的感应电流,则上滑时所受的安培力大于下滑时的安培力,由P=Fv知,经过同一位置时,上滑过程中杆克服安培力做功的功率大于下滑过程,上滑过程中电阻R的热功率大于下滑过程R的热功率.故D错误.
故选:BC
点评:本题分析杆的运动情况,比较同一位置安培力的大小是关键,再根据动量定理、安培力、能量守恒定律进行分析比较.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
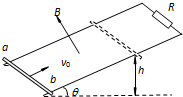 如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( )
如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( )| A、重力所做功的绝对值:上滑过程和下滑过程相等 | B、电阻R产生的热量:上滑过程比下滑过程少 | C、通过电阻R的电量:上滑比下滑过程多 | D、滑行时间:上滑过程比下滑过程短 |
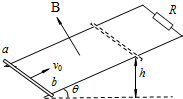 如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计轨道与金属杆ab的电阻及空气阻力,则( )
如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计轨道与金属杆ab的电阻及空气阻力,则( ) (2012?东城区一模)如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( )
(2012?东城区一模)如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( ) (2011?黄浦区一模)如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( )
(2011?黄浦区一模)如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速度v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则( )