题目内容
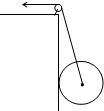如图所示，用一根轻质细绳通过小定滑轮拉着一个质量为m半径为R的实心球，当它沿光滑的竖直墙壁缓慢向上运动至某处时细绳断了，若绳所能承受的最大拉力为T（T＞G），求当球心距离定滑轮多远时球将要落下？（定滑轮半径忽略不计．）分析：实心球缓慢运动，所以处于平衡状态，对实心球受力分析，求出当绳子拉力为G时绳子与竖直方向夹角θ，然后由三角函数关系求出球心到定滑轮的距离
解答：解：设当球心距离定滑轮为L时球将要落下，设此时细绳与竖直墙壁的夹角为θ，
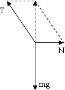
由力的平衡得：Tcosθ=G
根据上面的两个直角三角形由几何知识有：sinθ=
=
=
联立解得：L=
L=
答：当球心距离定滑轮
绳子会断．
由力的平衡得：Tcosθ=G
根据上面的两个直角三角形由几何知识有：sinθ=
| R |
| L |
| N |
| T |
| ||
| T |
联立解得：L=
| R |
| sinθ |
L=
| RT | ||
|
答：当球心距离定滑轮
| RT | ||
|
点评：物体处于共点力平衡时合力等于零，处理共点力平衡的方法有：合成法、正交分解法等．
练习册系列答案
相关题目
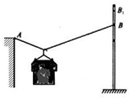（2010?山西模拟）如图所示，用一根轻质、光滑且不可伸长的绳子晾晒衣服，绳子的一端固定在墙角上的A点，另一端系在竖直杆上．通过光滑的挂钩将衣服悬挂在绳子上，并处于静止状态．现保持绳子的一端固定在A点不变，将另一端缓慢地沿竖直杆从B点向上移动到B1位置．在此过程中，下列判断正确的是（ ）
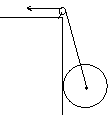如图所示，用一根轻质细绳通过小定滑轮拉着一个质量为m半径为R的实心球，当它沿光滑的竖直墙壁缓慢向上运动至某处时细绳断了，若绳所能承受的最大拉力为T（T>G），求当球心距离定滑轮多远时球将要落下？（定滑轮半径忽略不计.）
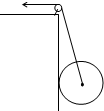如图所示，用一根轻质细绳通过小定滑轮拉着一个质量为m半径为R的实心球，当它沿光滑的竖直墙壁缓慢向上运动至某处时细绳断了，若绳所能承受的最大拉力为T（T＞G），求当球心距离定滑轮多远时球将要落下？（定滑轮半径忽略不计．）