题目内容
5．竖直悬挂的轻弹簧下连接一个小球，用手托起小球，使弹簧处于压缩状态，如图所示．则迅速放手后（ ）
| A． | 小球开始向下做匀加速运动 | B． | 弹簧恢复原长时小球加速度为零 | ||
| C． | 小球运动到最低点时加速度小于g | D． | 小球运动过程中最大加速度大于g |
分析 弹簧原来处于压缩状态，小球受到重力、弹簧向下的弹力和手的支持力，迅速放手后，分析小球的受力情况分析其运动情况，其中弹簧的弹力与弹簧的形变量大小成正比，根据牛顿第二定律研究小球的加速度．
解答 解：A、放手后，小球受到向下的重力和弹簧向下的弹力，由于弹力在变化，则合力在变化，加速度在变化，不是匀加速直线运动，故A错误．
B、弹簧恢复原长时，小球所受的合力为重力，加速度为g，故B错误．
C、小球松手后，在竖直方向上做简谐运动，最高点和最低点的加速度大小相等，最高点的加速度大小大于g，则最低点的加速度大于g，故C错误，D正确．
故选：D．
点评 本题关键是分析小球的受力情况，来判断其运动情况，利用简谐运动的对称性研究小球到达最低点时的加速度．
练习册系列答案
相关题目
2．一个质点做变速直线运动的v-t图象如图所示，下列说法中正确的是（ ）
| A． | 第1s内与第5s内的速度方向相反 | |
| B． | OA、AB、BC段的加速度aBC＞aOA＞aAB | |
| C． | 第5s末时质点刚好返回到出发点 | |
| D． | OA段的加速度与速度方向相同而BC段的加速度与速度方向相反 |
滚筒式静电分选器由料斗A，导板B，导体滚筒C，刮板D，料槽E、F和放电针G等部件组成，及分别接于直流高压电源的正、负极，并令C接地，如图所示，电源电压很高，足以使放电针G附近的空气发生电离并产生大量离子．现在导电性能不同的两种物质粉粒a、b混合物从料斗A下落，沿导板B到达转动的滚筒C上，粉粒a具有良好的导电性，粉粒b具有良好的绝缘性．
7．
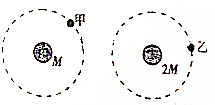如图所示，甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动，甲卫星的向心加速度、运行周期、角速度和线速度分别为a1、T1、ω1、v1，乙卫星的向心加速度、运行周期、角速度和线速度分别为a2、T2、ω2、v2，下列说法正确的是（ ）
如图所示，甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动，甲卫星的向心加速度、运行周期、角速度和线速度分别为a1、T1、ω1、v1，乙卫星的向心加速度、运行周期、角速度和线速度分别为a2、T2、ω2、v2，下列说法正确的是（ ）| A． | a1：a2=1：2 | B． | T1：T2=1：2 | C． | ω1：ω2=1：$\sqrt{2}$ | D． | v1：v2=$\sqrt{2}$：1 |
17．根据热力学第二定律，下列判断错误的是（ ）
| A． | 热机中，燃气内能不可能全部转化为机械能 | |
| B． | 一个物体的机械能不可能全部转化为内能 | |
| C． | 在火力发电机中，燃气的内能不可能全部转化为电能 | |
| D． | 在热传导中，热量不可能自发地从低温物体传递给高温物体，而不引起其它变化 |
15．如图甲所示，质量为2kg的绝缘板静止在粗糙水平地面上，质量为1kg、边长为1m、电阻为0.1Ω的正方形金属框ABCD位于绝缘板上，E、F分别为BC、AD的中点．某时刻起在ABEF区域内有竖直向下的磁场，其磁感应强度B1的大小随时间变化的规律如图乙所示，AB边恰在磁场边缘以外；FECD区域内有竖直向上的匀强磁场，磁感应强度B2=0.5T，CD边恰在磁场边缘以内．假设金属框受到的最大静摩擦力等于滑动摩擦力，两磁场均有理想边界，取g=10m/s2．则（ ）
| A． | 金属框中产生的感应电动势大小为1V | |
| B． | 金属框受到向左的安培力大小为2.5N | |
| C． | 金属框中的感应电流方向沿ADCB方向 | |
| D． | 如果金属框与绝缘板间的动摩擦因数为0.3，则金属框可以在绝缘板上保持静止 |