题目内容
如图所示,P点与R点关于坐标原点对称,距离为2a.有一簇质量为m、电量为q的离子,在xoy平面内,从P点以同一速率υ,沿与x轴成θ(0<θ<90)的方向射向同一个垂直于xoy平面的有界匀强磁场,磁感应强度为B,这些离子的运动轨迹对称于y轴,聚焦到R点.(1)求离子在磁场中运动的轨道半径r
(2)若离子在磁场中运动的轨道半径为a时,求与x轴成30°角射出的离子从P点到达R点的时间t
(3)试推出在x>0的区域中磁场的边界点坐标x与y之间满足的关系式.

【答案】分析:(1)离子进入磁场后,受到洛伦兹力作用做匀速圆周运动,根据向心力公式即可求解;
(2)先根据几何关系求出进入和离开磁场时的坐标,求出粒子运动的路程,根据时间等于路程除以速率求解;
(3)根据几何关系表示出x、y与半径r的关系,带入数据即可得出x与y之间满足的关系式.
解答:解: (1)离子进入磁场后,受到洛伦兹力作用,由牛顿第二定律得:
(1)离子进入磁场后,受到洛伦兹力作用,由牛顿第二定律得:

解得:
(2)如图所示,由对称性及几何关系可得,离子进入磁场A点坐标为:( ,
, )离开磁场B点坐标为:(
)离开磁场B点坐标为:( ,
, )
)
由几何关系,离子运动的路程为:
则:
(3)如图所示,设离子运动的轨道半径为r,在x>0的区域内,令离子离开磁场后与x轴夹角为θ.
由几何关系得:x=rsinθ

代入相关数据并化简得:
答:(1)求离子在磁场中运动的轨道半径r为 ;
;
(2)与x轴成30°角射出的离子从P点到达R点的时间t为 ;
;
(3)在x>0的区域中磁场的边界点坐标x与y之间满足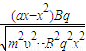 .
.
点评:本题是带电粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,结合几何关系求解,知道半径公式及周期公式,难度较大.
(2)先根据几何关系求出进入和离开磁场时的坐标,求出粒子运动的路程,根据时间等于路程除以速率求解;
(3)根据几何关系表示出x、y与半径r的关系,带入数据即可得出x与y之间满足的关系式.
解答:解:
 (1)离子进入磁场后,受到洛伦兹力作用,由牛顿第二定律得:
(1)离子进入磁场后,受到洛伦兹力作用,由牛顿第二定律得:
解得:

(2)如图所示,由对称性及几何关系可得,离子进入磁场A点坐标为:(
 ,
, )离开磁场B点坐标为:(
)离开磁场B点坐标为:( ,
, )
)由几何关系,离子运动的路程为:

则:

(3)如图所示,设离子运动的轨道半径为r,在x>0的区域内,令离子离开磁场后与x轴夹角为θ.
由几何关系得:x=rsinθ


代入相关数据并化简得:

答:(1)求离子在磁场中运动的轨道半径r为
 ;
;(2)与x轴成30°角射出的离子从P点到达R点的时间t为
 ;
;(3)在x>0的区域中磁场的边界点坐标x与y之间满足
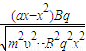 .
.点评:本题是带电粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,结合几何关系求解,知道半径公式及周期公式,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
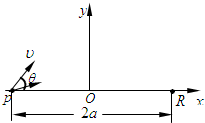 如图所示,P点与R点关于坐标原点对称,距离为2a.有一簇质量为m、电量为q的离子,在xoy平面内,从P点以同一速率υ,沿与x轴成θ(00<θ<900)的方向射向同一个垂直于xoy平面的有界匀强磁场,磁感应强度为B,这些离子的运动轨迹对称于y轴,聚焦到R点.
如图所示,P点与R点关于坐标原点对称,距离为2a.有一簇质量为m、电量为q的离子,在xoy平面内,从P点以同一速率υ,沿与x轴成θ(00<θ<900)的方向射向同一个垂直于xoy平面的有界匀强磁场,磁感应强度为B,这些离子的运动轨迹对称于y轴,聚焦到R点.

 如图所示,P点与R点关于坐标原点对称,距离为2a。有一簇质量为m、电量为q的离子,在
如图所示,P点与R点关于坐标原点对称,距离为2a。有一簇质量为m、电量为q的离子,在