题目内容
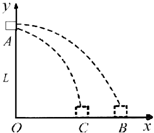 如图为俯视图,在一光滑水平面上建立x-y平面直角坐标系.有一质量为m的小木块从A点沿x轴方向以某初速度射出,A点离x轴距离为L,小木块沿y轴负方向始终受到恒力F1=F0.小木块的运动轨迹与x轴的交点B到y轴距离为S;当同时施加沿x轴负方向恒力F2时,小木块仍以原来初速度射出,其运动轨迹与x轴的交点C到y轴距离为
如图为俯视图,在一光滑水平面上建立x-y平面直角坐标系.有一质量为m的小木块从A点沿x轴方向以某初速度射出,A点离x轴距离为L,小木块沿y轴负方向始终受到恒力F1=F0.小木块的运动轨迹与x轴的交点B到y轴距离为S;当同时施加沿x轴负方向恒力F2时,小木块仍以原来初速度射出,其运动轨迹与x轴的交点C到y轴距离为| 3 | 4 |
(1)求小木块初速度v0的大小;
(2)求恒力F2与F1的比值.
分析:(1)根据类平抛运动的规律,分成竖直方向和水平方向进行分解运动,然后即可求出初速度;
(2)因为水平初速度不变,根据竖直位移求出时间,然后即可求出水平方向的加速度,根据牛顿第二定律即可解得F2.
(2)因为水平初速度不变,根据竖直位移求出时间,然后即可求出水平方向的加速度,根据牛顿第二定律即可解得F2.
解答:解(1)分析A到B过程有:
竖直方向:L=
at2=
t2
s=v0t
解方程得:v0=s
(2)设小木块到x轴时沿x轴方向上的速度为vx,
分析x轴,由匀变速直线运动的规律得:
vx=v0-
t
即
s=
t①
又因为L=
t2②
由①②
=
即
=
.
答:(1)求小木块初速度v0的大小为s
;
(2)求恒力F2与F1的比值为
.
竖直方向:L=
| 1 |
| 2 |
| 1 |
| 2 |
| F0 |
| m |
s=v0t
解方程得:v0=s
|
(2)设小木块到x轴时沿x轴方向上的速度为vx,
分析x轴,由匀变速直线运动的规律得:
vx=v0-
| F2 |
| m |
即
| 3 |
| 4 |
| v0+v |
| 2 |
又因为L=
| 1 |
| 2 |
| F0 |
| m |
由①②
| F2 |
| F0 |
| s |
| 4L |
即
| F2 |
| F1 |
| s |
| 4L |
答:(1)求小木块初速度v0的大小为s
|
(2)求恒力F2与F1的比值为
| s |
| 4L |
点评:本题主要考察了类平抛运动的合成和分解,并熟练运用动能定理解答做功问题,解答此题的关键是类比为平抛运动然后进行分析解答即可.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 A.(选修模块3-3)
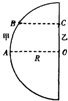
A.(选修模块3-3)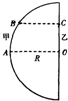 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?


 A.(选修模块3-3)
A.(选修模块3-3) D3,则在该状态下体积为V的二氧化碳气体变成固体后体积为多少?
D3,则在该状态下体积为V的二氧化碳气体变成固体后体积为多少? (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少? →
→ .若
.若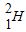 和
和 迎面碰撞,初速度大小分别为v1、v2,
迎面碰撞,初速度大小分别为v1、v2, 、
、 、
、 He、
He、 的质量分别为m1、m2、m3、m4,反应后
的质量分别为m1、m2、m3、m4,反应后 He的速度大小为v3,方向与
He的速度大小为v3,方向与 的运动方向相同,求中子
的运动方向相同,求中子 的速度
的速度