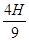题目内容
小球由地面竖直上抛,上升最大高度为H,设所受空气阻力大小恒定,地面为零势能面,在上升至离地面高度h处,小球动能为势能的2倍,在下落至离地面高度h处,小球势能是动能的2倍,求h是H的多少倍.
分析:小球上升和下降过程反复应用功能原理,并且在h处表达动能和势能的数量关系,联立方程组问题可解.
解答:解:设初动能为Ek0,阻力大小为f,上升至离地h时动能为Ek1,下落至离地h时动能为Ek2,
那么由功能关系可知,任何阶段减少的机械能都等于克服摩擦力做的功.
故有:
从抛出到上升到最大高度的过程,有
Ek0-mgH=fH ①
从抛出到上升到高度h处的过程,有
Ek0-(mgh+Ek1)=fh ②
从抛出到下落到高度h处的全过程,有
Ek0-(mgh+Ek2)=f(2H-h) ③
题知:Ek1=2mgh ④
Ek2=
mgh ⑤
联接①②③④⑤得 h=
H ⑥
答:h是H的
倍.
那么由功能关系可知,任何阶段减少的机械能都等于克服摩擦力做的功.
故有:
从抛出到上升到最大高度的过程,有
Ek0-mgH=fH ①
从抛出到上升到高度h处的过程,有
Ek0-(mgh+Ek1)=fh ②
从抛出到下落到高度h处的全过程,有
Ek0-(mgh+Ek2)=f(2H-h) ③
题知:Ek1=2mgh ④
Ek2=
| 1 |
| 2 |
联接①②③④⑤得 h=
| 4 |
| 9 |
答:h是H的
| 4 |
| 9 |
点评:在应用动能定理解题时,各个力的做功分析非常重要,本题中上升和下降过程中阻力始终做负功是关键.

练习册系列答案
相关题目
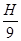 B.
B.  C.
C.  D.
D.