题目内容
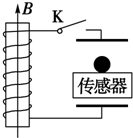如图所示，两块水平放置的金属板距离为d，用导线、开关K与一个n匝的线圈连接，线圈置于方向竖直向上的变化磁场B中．两板间放一台小压力传感器，压力传感器上表面静止放置一个质量为m、电荷量为+q的小球，K断开时传感器上有示数，K闭合稳定后传感器上恰好无示数，则线圈中的磁场B的变化情况和磁通量变化率分别是（ ）A、正在增加，
| ||||
B、正在减弱，
| ||||
C、正在减弱，
| ||||
D、正在增加，
|
分析：线圈置于方向竖直向上的均匀变化的磁场中，根据法拉第电磁感应定律E=n
，可知线圈中会产生稳定的电动势．当电键断开时，小球受重力和支持力平衡，当电键闭合时，支持力变为mg，可知，小球受到向上的电场力，根据小球的平衡可求出磁通量的变化率以及磁场的变化．
| △Φ |
| △t |
解答：解：电键闭合时有：qE=mg，
解得：E=
又E=
解得：
=
小球带正电，知上极板带负电，根据楞次定律得知，磁场正在增强
故D正确、ABC错误．
故选：D．
解得：E=
| mg |
| q |
又E=
| U |
| d |
解得：
| △Φ |
| △t |
| mgd |
| nq |
小球带正电，知上极板带负电，根据楞次定律得知，磁场正在增强
故D正确、ABC错误．
故选：D．
点评：解决本题的关键掌握法拉第电磁感应定律E=n
，以及会用楞次定律判端电动势的方向．
| △Φ |
| △t |
练习册系列答案
阅读快车系列答案
相关题目
气垫导轨是常用的一种实验仪器，它是利用气泵使带孔的导轨与滑块之间形成气垫，使滑块悬浮在导轨上，滑块在导轨上的运动可视为没有摩擦．用带有刻度尺和感应计时器及竖直挡板C和D的气垫导轨和滑块A和B验证动量守恒定律，实验装置如图所示，采用的实验步骤如下：
