题目内容
14. 如图所示,AB为水平轨道,A、B间距离s,BCD是半径为R的竖直光滑半圆形轨道,B为两轨道的连接点,D为轨道的最高点,一质量为m的小物块在水平恒力的作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,小物块与水平轨道间动摩擦因数为μ,重力加速度为g.求:
如图所示,AB为水平轨道,A、B间距离s,BCD是半径为R的竖直光滑半圆形轨道,B为两轨道的连接点,D为轨道的最高点,一质量为m的小物块在水平恒力的作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,小物块与水平轨道间动摩擦因数为μ,重力加速度为g.求:(1)小物块从D点落回水平轨道时到B点的距离;
(2)小物块运动到B点时速度大小;
(3)水平恒力F的大小.
分析 (1)物块做圆周运动,由牛顿第二定律求出到达D点的速度,离开D后物块做平抛运动,应用平抛运动规律可以求出水平位移.
(2)从B到D机械能守恒,应用机械能守恒定律可以求出到达B点的速度.
(3)从A到B,应用动能定理可以求出拉力F.
解答 解:(1)设小物块刚好到达D点时速度为vD,
在D点,由牛顿第二定律得:mg=m$\frac{{v}_{D}^{2}}{R}$,
小物块离开D点后做平抛运动,
竖直方向:2R=$\frac{1}{2}$gt2,
水平方向:x=vDt,
解得:x=2R;
(2)设小物块运动到B点时速度为vB,
小物块由B运动到D点过程机械能守恒,
$\frac{1}{2}$mvB2=$\frac{1}{2}$mvD2+mg•2R,解得:vB=$\sqrt{5gR}$;
(3)从A到B过程,由动能定理得:
(F-μmg)s=$\frac{1}{2}$mvB2-0,解得:F=μmg+$\frac{5mgR}{2s}$;
答:(1)小物块从D点落回水平轨道时到B点的距离为2R;
(2)小物块运动到B点时速度大小为$\sqrt{5gR}$;
(3)水平恒力F的大小为μmg+$\frac{5mgR}{2s}$.
点评 本题是一道力学综合题,分析清楚物体运动过程,应用牛顿第二定律、平抛运动规律、机械能守恒定律与动能定理可以解题.

练习册系列答案
相关题目
4. 将静止在地面上,质量为20kg的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示,以下判断正确的是( )
将静止在地面上,质量为20kg的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示,以下判断正确的是( )
 将静止在地面上,质量为20kg的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示,以下判断正确的是( )
将静止在地面上,质量为20kg的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示,以下判断正确的是( )| A. | 前3s内货物重力势能增加了360J | |
| B. | 整个7s过程中外力对货物做的总功为零 | |
| C. | 第3s末至第5s末的过程中,货物的机械能守恒 | |
| D. | 第5s末至第7s末的过程中,货物的机械能减少 |
5. 如图甲所示,长为L的轻杆一端固定一小球,可绕另一端O点在竖直平面内转动.小球运动到最高点时,速度大小为v,杆与小球间弹力大小为F,其F-v2图象如图乙所示,g取10m/s2,则( )
如图甲所示,长为L的轻杆一端固定一小球,可绕另一端O点在竖直平面内转动.小球运动到最高点时,速度大小为v,杆与小球间弹力大小为F,其F-v2图象如图乙所示,g取10m/s2,则( )
 如图甲所示,长为L的轻杆一端固定一小球,可绕另一端O点在竖直平面内转动.小球运动到最高点时,速度大小为v,杆与小球间弹力大小为F,其F-v2图象如图乙所示,g取10m/s2,则( )
如图甲所示,长为L的轻杆一端固定一小球,可绕另一端O点在竖直平面内转动.小球运动到最高点时,速度大小为v,杆与小球间弹力大小为F,其F-v2图象如图乙所示,g取10m/s2,则( )| A. | 当v2<4时,杆对小球的弹力方向向下 | |
| B. | 当v2=4时,杆对小球的弹力等于小球重力 | |
| C. | 小球的质量为2.5kg | |
| D. | 杆的长度为0.4m |
2. 如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
 如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )| A. | 减小R2的阻值,b点的电势升高 | |
| B. | 当煤气的浓度升高时,b点的电势升高 | |
| C. | 适当减小ac间的电压,可以提高报警器的灵敏度 | |
| D. | 调节R2的阻值能改变报警器启动时煤气浓度的临界值 |
9.已知地球表面处的重力加速度为g,则在距地面高度为地球半径3倍处的重力加速度为( )
| A. | $\frac{g}{16}$ | B. | $\frac{g}{9}$ | C. | 3g | D. | 4g |
19.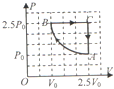 一定质量理想气体经历如图所示的A→B、B→C、C→A三个变化过程,AB为双曲线的一支,则下列说法正确的是( )
一定质量理想气体经历如图所示的A→B、B→C、C→A三个变化过程,AB为双曲线的一支,则下列说法正确的是( )
 一定质量理想气体经历如图所示的A→B、B→C、C→A三个变化过程,AB为双曲线的一支,则下列说法正确的是( )
一定质量理想气体经历如图所示的A→B、B→C、C→A三个变化过程,AB为双曲线的一支,则下列说法正确的是( )| A. | A→B过程气体向外放热 | |
| B. | B→C过程气体对外界做功 | |
| C. | C→A过程气体内能增加 | |
| D. | 若气体在状态A的温度为100℃,则状态C的温度为250℃ |
6.关于电磁波下列说法正确的是( )
| A. | 赫兹最早预言了电磁波的存在 | B. | 紫外线具有荧光效应,可用来验钞 | ||
| C. | X射线的波长比红外线长 | D. | 电磁波传递能量但不能传递信息 |
3. 倾角为α的斜劈A静止放置在水平地面上,质量为m的物体B以一定的初速度V沿斜面下滑,已知物体B与斜面劈A间的动摩擦因数为tanα,则下列说法正确的是( )
倾角为α的斜劈A静止放置在水平地面上,质量为m的物体B以一定的初速度V沿斜面下滑,已知物体B与斜面劈A间的动摩擦因数为tanα,则下列说法正确的是( )
 倾角为α的斜劈A静止放置在水平地面上,质量为m的物体B以一定的初速度V沿斜面下滑,已知物体B与斜面劈A间的动摩擦因数为tanα,则下列说法正确的是( )
倾角为α的斜劈A静止放置在水平地面上,质量为m的物体B以一定的初速度V沿斜面下滑,已知物体B与斜面劈A间的动摩擦因数为tanα,则下列说法正确的是( )| A. | 若此刻加一竖直向下的恒力作用在物体B上,物体B一定加速下滑 | |
| B. | 若此刻对物体B施加一水平向左的推力,则地面对斜劈A无摩擦力 | |
| C. | 若此刻对物体B施加一水平向左的推力,则地面对斜劈的摩擦力向右 | |
| D. | 若此刻对物体B施加一平行于斜面向下的恒定推力,物体B加速下滑 |
