题目内容
17.物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零,一个质量为m0的质点到质量为M0的引力源中心的距离为r0时,其万有引力势能Ep=-$\frac{{{GM}_{0}m}_{0}}{{r}_{0}}$(式中G为引力常数).一颗质量为m的人造地球卫星以半径为r1的圆形轨道环绕地球匀速飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为(假设卫星的质量始终不变,不计空气阻力及其它星体的影响)( )| A. | E=$\frac{GMm}{2}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | B. | E=GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | ||
| C. | E=$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | D. | E=$\frac{2GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$)我 |
分析 求出卫星在半径为r1圆形轨道和半径为r2的圆形轨道上的动能,从而得知动能的减小量,通过引力势能公式求出势能的增加量,根据能量守恒求出发动机所消耗的最小能量.
解答 解:卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,卫星绕地球运动的动能:EK=$\frac{1}{2}$mv2=$\frac{GMm}{2r}$,
由能量守恒定律可知,卫星轨道发生变化时,发电机消耗的最小能量:E=△EK+△EP=EK2-EK1+EP2-EP1=$\frac{GMm}{2}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$);
故选:A.
点评 本题考查了求发电机消耗的能量,本题是一道信息给予题,认真审题,从题目获取所需信息是正确解题的前提,解决本题的关键得出卫星动能和势能的变化量,从而根据能量守恒进行求解.

练习册系列答案
相关题目
8.一般物质分子非常小,分子质量也非常小,科学家采用摩尔为物质的量的单位,实现了微观物理量与宏观物理量间的换算.1摩尔的任何物质都含有相同的粒子数,这个数量为称阿伏伽德罗常数NA,通过下列条件可以得出阿伏伽德罗常数的是( )
| A. | 己知水分子的体枳和水的摩尔质量 | |
| B. | 己知水的摩尔质量和水分子的质量 | |
| C. | 已知氧气分子的质量和氧气的摩尔质量 | |
| D. | 己知氧气分子的体积和氧气的摩尔体积 |
12.关于磁感线下列说法正确的是( )
| A. | 磁感线是磁场中实际存在的线 | |
| B. | 条形磁铁磁感线只分布于磁铁外部 | |
| C. | 当空中存在几个磁场时,磁感线有可能相交 | |
| D. | 磁感线上某点的切线方向就是放在这里的小磁针N极受力的方向 |
2.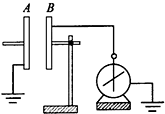 如图所示,平行板电容器的极板B固定且与静电计相连,极板A可以自由移动,现使电容器带电后与电源断开,静电计的指针偏转一定角度.若整个装置放在真空的环境里,以下操作能使静电计指针的偏转角变大的是( )
如图所示,平行板电容器的极板B固定且与静电计相连,极板A可以自由移动,现使电容器带电后与电源断开,静电计的指针偏转一定角度.若整个装置放在真空的环境里,以下操作能使静电计指针的偏转角变大的是( )
 如图所示,平行板电容器的极板B固定且与静电计相连,极板A可以自由移动,现使电容器带电后与电源断开,静电计的指针偏转一定角度.若整个装置放在真空的环境里,以下操作能使静电计指针的偏转角变大的是( )
如图所示,平行板电容器的极板B固定且与静电计相连,极板A可以自由移动,现使电容器带电后与电源断开,静电计的指针偏转一定角度.若整个装置放在真空的环境里,以下操作能使静电计指针的偏转角变大的是( )| A. | 将极板A向右水平移动一小段距离 | B. | 将极板A向左水平移动一小段距离 | ||
| C. | 将极板A向上竖直移动一小段距离 | D. | 在极板A、B间插入电介质 |
9. 回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(${\;}_{1}^{3}H$)加速,下列说法正确的是( )
回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(${\;}_{1}^{3}H$)加速,下列说法正确的是( )
 回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(${\;}_{1}^{3}H$)加速,下列说法正确的是( )
回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(${\;}_{1}^{3}H$)加速,下列说法正确的是( )| A. | 加速器所加交流电源的周期与粒子在磁场中运动的周期相同 | |
| B. | 引出粒子的动能与加速电压有关 | |
| C. | 引出粒子的动能与D形金属盒半径有关 | |
| D. | 引出粒子的动能与磁感应强度B有关 |
6.下列说法正确的有( )
| A. | 普朗克曾经大胆假设:振动着的带电微粒的能量只能是某一最小能量值e的整数倍,这个不可再分的最小能量值e叫做能量子 | |
| B. | 卢瑟福根据α粒子散射实验的实验现象,提出了原子的核式结构模型 | |
| C. | 由波尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要吸收一定频率的光子,光子的能量是分立的 | |
| D. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子的最大初动能E0越大,则这种金属的逸出功W0越小 | |
| E. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变短. |
7.一物体静止在升降机的地板上,在升降机加速上升的过程中,地板对物体的支持力所做的功等于( )
| A. | 物体重力势能的增加量 | |
| B. | 物体动能的增加量 | |
| C. | 物体动能的增加量加上物体重力势能的增加量 | |
| D. | 物体动能的增加量加上克服重力所做的功 |
 (1)下列现象中,能说明液体存在表面张力的有AB.
(1)下列现象中,能说明液体存在表面张力的有AB. 如图所示,两端开口的汽缸水平固定,A、B是两个厚度不计的活塞,面积分别为S1=20cm2,S2=10cm2,它们之间用一根细杆连接,B通过水平细绳绕过光滑的定滑轮与质量为M的重物C连接,静止时汽缸中的空气压强p1=1.2atm,温度T1=600K,汽缸两部分的气柱长均为L.已知大气压强p0=1atm=1.0×105 Pa,取g=10m/s2,缸内空气可看做理想气体,不计摩擦.求:
如图所示,两端开口的汽缸水平固定,A、B是两个厚度不计的活塞,面积分别为S1=20cm2,S2=10cm2,它们之间用一根细杆连接,B通过水平细绳绕过光滑的定滑轮与质量为M的重物C连接,静止时汽缸中的空气压强p1=1.2atm,温度T1=600K,汽缸两部分的气柱长均为L.已知大气压强p0=1atm=1.0×105 Pa,取g=10m/s2,缸内空气可看做理想气体,不计摩擦.求: