题目内容
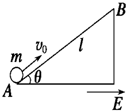如图所示，长为L，倾角为θ的光滑绝缘斜面处于水平向右的匀强电场中，一电荷量为+q，质量为m的小球，以初速度v0从斜面底端A点开始沿斜面上滑，当达到斜面顶端的B点时，速度仍为v0，电场强度E=| mg |
| q |
| mg |
| q |
分析：带电小球从底端运动到顶端的过程中受：重力、支持力、电场力，由动能定理可以求出电场强度．
解答：解：在小球从A到B的过程中，由动能定理可得：
-mgLsinθ+qELcosθ=
mv02 -
mv02，
解得：E=
tanθ；
故答案为：
tanθ．
-mgLsinθ+qELcosθ=
| 1 |
| 2 |
| 1 |
| 2 |
解得：E=
| mg |
| q |
故答案为：
| mg |
| q |
点评：本题考查了求电场强度的问题，对带电小球正确受力分成，应用动能定理即可正确解题，本题难度不大，是一道基础题．
练习册系列答案
发散思维新课堂系列答案
相关题目
，从某一高处水平抛出，到A点时速度方向恰沿AB方向，并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数
（g取10m/s2，
）求：