题目内容
欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位.现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，轨道半径为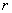
，一个轨道平面上某时刻10颗卫星所在位置分布如图所示．其中卫星1和卫星3分别位于轨道上的A、B两位置．若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中正确的是（ ）
A．这10颗卫星的加速度大小相等，均为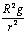
B．卫星1向后喷气就一定能追上卫星2
C．卫星1由位置A运动到位置B所需的时间为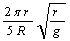
D．卫星1由位置A运动到位置B的过程中万有引力做功不为零
【答案】
AC
【解析】
试题分析：根据万有引力提供向心力可得由公式
得
，再根据黄金替代公式
,带入可得
，A正确，卫星在原轨道上向后喷气，速度增大，万有引力不够提供向心力，会做离心运动，离开原轨道．所以不会追上．故B错误，根据万有引力提供向心力，由公式
得
，，所以时间
，C正确，卫星1由位置A运动到位置B的过程中万有引力和速度方向总是垂直的，所以做功为零，D错误，
考点：考查了对同步卫星的理解
点评：本题是卫星类型的问题，常常建立这样的模型：环绕天体绕中心天体做匀速圆周运动，由中心天体的万有引力提供向心力．
练习册系列答案
相关题目
欧盟和我国合作的“伽利略”全球卫星定位系统的空间部分由平均分布在三个轨道平面上的30颗轨道卫星构成，每个轨道平面上有10颗卫星，从而实现高精度的导航定位．现假设“伽利略”系统中每颗卫星均绕地心O做半径为r的匀速圆周运动，某时刻10颗卫星所在位置如图所示，相邻卫星之间的距离相等，卫星1和卫星3分别位于A、B两位置，卫星按顺时针运行．地球表面重力加速度为g，地球的半径为R．求卫星1由A位置运行到B位置所需要的时间．
欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位，现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，一个轨道平面上某时刻10颗卫星所在位置分布（如图）所示．若卫星均顺时针运行，地球表面处的重力加速度为g，不计卫星间的相互作用力．则以下判断中错误的是（ ）
（2008?宿迁模拟）欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位．现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，轨道半径为r，一个轨道平面上某时刻10颗卫星所在位置分布如图所示．其中卫星1和卫星3分别位于轨道上的A、B两位置．若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中正确的是（ ）
欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位．现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，轨道半径为r，一个轨道平面上某时刻10颗卫星所在位置分布如图所示．其中卫星1和卫星3分别位于轨道上的A、B两位置．若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中正确的是（ ）
欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位，现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，一个轨道平面上某时刻10颗卫星所在位置分布如图所示．若卫星均顺时针运行，地球表面处的重力加速度为g，不计卫星间的相互作用力．则以下判断中正确的是（ ）