题目内容
8. 如图所示,点电荷A和B带电荷量分别为3.0×10-8C和-2.4×10-8C,彼此相距60cm.若在两点电荷连线中点O处放一个半径为5cm的金属球壳,则球壳上感应电荷在该O处产生的电场强度大小为5.4×103 N/C,方向水平向左.
如图所示,点电荷A和B带电荷量分别为3.0×10-8C和-2.4×10-8C,彼此相距60cm.若在两点电荷连线中点O处放一个半径为5cm的金属球壳,则球壳上感应电荷在该O处产生的电场强度大小为5.4×103 N/C,方向水平向左.
分析 当导体处于静电平衡状态时,导体内部场强处处为零,球壳上感应电荷在球心O处产生的场强与外电场在O点的场强大小相等,方向相反.只要求出两个点电荷在球心O处产生的合场强,即可得到球壳上感应电荷在球心O处产生的电场强度.
解答 解:两个点电荷在O处产生的场强为:
E=$\frac{k{q}_{1}}{{r}_{1}^{2}}$+$\frac{k{q}_{2}}{{r}_{2}^{2}}$=($\frac{9×1{0}^{9}×3×1{0}^{-8}}{0.{3}^{2}}$+$\frac{9×1{0}^{9}×2.4×1{0}^{-8}}{0.{3}^{2}}$)N/C=5.4×103N/C,方向水平向右.
根据静电平衡状态的特点可知,球壳上感应电荷在球心O处产生的电场强度与两个点电荷在O处产生的电场强度大小相等,方向相反,所以球壳上感应电荷在球心O处产生的电场强度大小为:
E′=E=5.4×103N/C,方向水平向左.
故答案为:5.4×103,水平向左.
点评 解决本题的关键知道静电平衡导体的特点:内部场强处处为零,即外加电场和感应电荷产生电场的合场强为零.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
19.关于加速度,下述说法中不正确的是( )
| A. | 加速度用来表示物体速度变化的快慢 | |
| B. | 加速度方向与速度方向可能相同,也可能相反 | |
| C. | 加速度很大时物体速度可能很小 | |
| D. | 加速度大的物体速度变化一定很大 |
 如图所示,有一水平方向的匀强电场,场强大小为9×103N/C,在电场内一水平面上作半径10cm的圆,圆周上取A、B两点,AO连线沿E方向,BO⊥AO,另在圆心O处放一电量为10-8C的正点电荷,则A处场强大小EA=0,B处场强的大小EB=9$\sqrt{2}$×103N/C,方向为与水平方向成45°角斜向右下方.
如图所示,有一水平方向的匀强电场,场强大小为9×103N/C,在电场内一水平面上作半径10cm的圆,圆周上取A、B两点,AO连线沿E方向,BO⊥AO,另在圆心O处放一电量为10-8C的正点电荷,则A处场强大小EA=0,B处场强的大小EB=9$\sqrt{2}$×103N/C,方向为与水平方向成45°角斜向右下方.
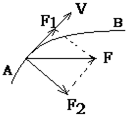 物体做曲线运动时轨迹与所受的合外力F的情况如图,我们将力F分解得与v共线的力F1、与v垂直的力F2,讨论其中F1、F2的作用.
物体做曲线运动时轨迹与所受的合外力F的情况如图,我们将力F分解得与v共线的力F1、与v垂直的力F2,讨论其中F1、F2的作用.