题目内容
8．
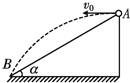如图所示，在倾角为α=37°的斜坡顶端A处，沿水平方向以初速度v0=10m/s抛出一小球，恰好落在斜坡的B点，取重力加速度g=10m/s2，求：（1）小球在空中飞行的时间；
（2）AB间的距离．
分析 小球做的是平抛运动，研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，两个方向上运动的时间相同，由此列式即可求解．
解答 解：设小球的飞行时间为t．A、B之间的距离为sAB，
由题中图可知：sABcos α=v0t…①
sAB•sin α=$\frac{1}{2}$gt2…②
由①②两式解得：t=$\frac{2{v}_{0}tanα}{g}$
代入数据得：t=1.5s．
将时间t代入①得：sAB=18.75 m
答：（1）小球在空中飞行的时间是1.5s；
（2）AB间的距离是18.75m．
点评 本题就是对平抛运动规律的考查，平抛运动可以分解为在水平方向上的匀速直线运动，和竖直方向上的自由落体运动来求解．
练习册系列答案
相关题目
19．
空降兵某部官兵使用新装备进行超低空跳伞训练．若跳伞空降兵在离地面224m高处由静止开始在竖直方向做自由落体运动．-段时间后立即打开降落伞，以12.5m/s2的平均加速度匀减速下降．为了空降兵的安全，要求空降兵落地速度最大不得超过5m/s（g取10m/s2）．则（ ）
空降兵某部官兵使用新装备进行超低空跳伞训练．若跳伞空降兵在离地面224m高处由静止开始在竖直方向做自由落体运动．-段时间后立即打开降落伞，以12.5m/s2的平均加速度匀减速下降．为了空降兵的安全，要求空降兵落地速度最大不得超过5m/s（g取10m/s2）．则（ ）| A． | 空降兵展开伞时离地面高度至少为125m | |
| B． | 空降兵展开伞时离地面高度至少为99m | |
| C． | 空降兵落地落地相当于从1.25m高处自由落下 | |
| D． | 空降兵落地落地相当于从2.5m高处自由落下 |
16．如图所示是某质点运动的速度图象，由图象得到的正确结果是（ ）
| A． | 0～1s内的平均速度是2m/s | |
| B． | 0～2s内的位移大小是3m | |
| C． | 0～1s内的加速度小于2～4s内的加速度 | |
| D． | 0～4s内物体平均速度0m/s |
20．下列说法正确的是（ ）
| A． | 施力物体同时也一定是受力物体 | |
| B． | 只有相互接触的物体间才能产生力的作用 | |
| C． | 物体的重心就是物体上最重的一点 | |
| D． | 重力方向一定垂直于地面向下 |
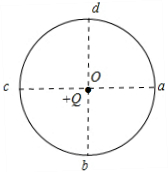
如图所示，一束带负电的粒子（质量为m、电荷量为e）以速度v垂直磁场的边界从A点射入磁感应强度为B、宽度为d的匀强磁场中．若粒子的速度大小可变．方向不变，要使粒子不能通过磁场的右边界，则粒子的速度最大不能超过多少？