题目内容
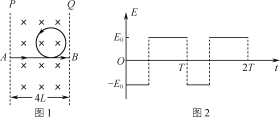
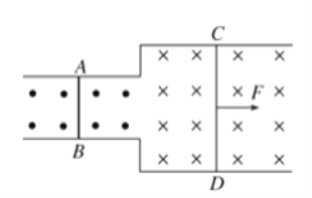
【题目】如图所示,两根质量均为m的金属棒垂直地放在光滑的水平导轨上,左、右两部分导轨间距之比为1∶2,导轨间左、右两部分有大小相等、方向相反的匀强磁场,两棒电阻与棒长成正比,不计导轨电阻,现用水平恒力F向右拉CD棒,在CD棒向右运动距离为s的过程中,AB棒上产生的焦耳热为Q,此时AB棒和CD棒的速度大小均为v,此时立即撤去拉力F,设导轨足够长且两棒始终在不同磁场中运动,则下列说法正确的是( )
A.v的大小等于![]()
B.撤去拉力F后,AB棒的最终速度大小为![]() v,方向向右
v,方向向右
C.撤去拉力F后,CD棒的最终速度大小为![]() v,方向向右
v,方向向右
D.撤去拉力F后,整个回路产生的焦耳热为![]() mv2
mv2
【答案】AC
【解析】
A.两棒的长度之比为1:2,所以电阻之比为1:2,由于电路在任何时刻电流均相等,根据焦耳定律:Q=I2Rt,所以CD棒的焦耳热为2Q,在CD棒向右运动距离为s的过程中,根据功能关系有
![]()
解得
![]()
故A正确;
BC.令AB棒的长度为l,则CD棒长为2l,撤去拉力F后,AB棒继续向左加速运动,而CD棒向右开始减速运动,两棒最终匀速运动时,电路中电流为零,两棒切割磁感线产生的感应电动势大小相等,此时两棒的速度满足
BlvAB′=B2lvCD′
即
vAB′=2vCD′
对两棒分别应用动量定理,有
FABt=mvAB′-mv
-FCDt=mvCD′-mv
因为
FCD=2FAB
所以
vAB′=![]() v
v
vCD′=![]() v
v
故B错误,C正确;
D.撤去外力F到最终稳定运动过程根据能量守恒定律
![]()
故D错误。
故选AC。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目