题目内容
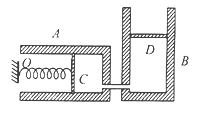
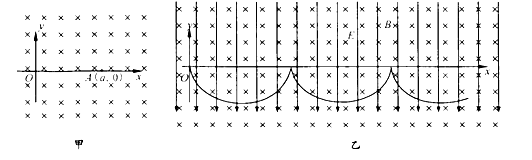
【题目】如图甲所示,空间存在一范围足够大、方向垂直于竖直xOy平面向里的匀强磁场,磁感应强度大小为B。让质量为m,电荷量为q(q>0)的粒子从坐标原点O沿xOy平面入射。不计粒子重力,重力加速度为g。
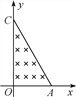
(1)若该粒子沿y轴负方向入射后,恰好能经过x轴上的A(a,0)点,求粒子速度![]() 的大小。
的大小。
(2)若该粒子以速度v沿y轴负方向入射的同时,一不带电的小球从x轴上方某一点平行于x轴向右抛出,二者经过时![]() 恰好相遇,求小球抛出点的纵坐标。
恰好相遇,求小球抛出点的纵坐标。
(3)如图乙所示,在此空间再加入沿y轴负方向、大小为E的匀强电场,让该粒子改为从O点静止释放,研究表明:粒子在xOy平面内将做周期性运动,其周期![]() ,且在任一时刻,粒子速度的水平分量
,且在任一时刻,粒子速度的水平分量![]() 与其所在位置的y轴坐标绝对值的关系为
与其所在位置的y轴坐标绝对值的关系为![]() 。若在粒子释放的同时,另有一不带电的小球从x轴上方某一点平行于x轴向右抛出,二者经过时间
。若在粒子释放的同时,另有一不带电的小球从x轴上方某一点平行于x轴向右抛出,二者经过时间![]() 恰好相遇,求小球抛出点的纵坐标。
恰好相遇,求小球抛出点的纵坐标。
【答案】(1)![]() (2)
(2)![]()
(3)![]()
【解析】
试题分析:(1)由题意可知,粒子做匀速圆周运动的半径为![]() ,有:
,有:![]()
洛伦兹力提供向心力,有:![]()
解得:![]()
(2)洛伦兹力提供向心力,又有:![]()
解得:![]()
粒子做匀速圆周运动的周期为![]() ,有:
,有:![]()
则相遇时间为:![]()
在这段时间内粒子转动的圆心角为![]() ,有:
,有:![]()
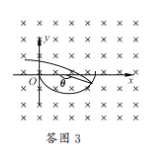
如图3所示,相遇点的纵坐标绝对值为:![]()
小球跑出点的纵坐标为:![]()
(3)相遇时间![]() ,
,
由对称性可知相遇点在第二个周期运动的最低点
设粒子运动到最低点时,离![]() 轴的距离为
轴的距离为![]() ,水平速度为
,水平速度为![]()
由动能定理,有:![]()
联立解得:![]()
故小球抛出点的纵坐标为:![]()

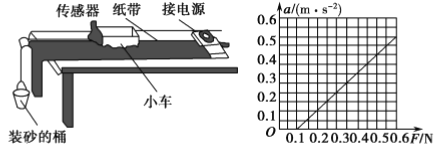
【题目】某实验小组采用如图所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行。打点计时器的工作频率为50 Hz。
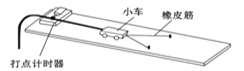
(1)实验中木板略微倾斜,这样做_________;
A.是为了使释放小车后,小车能匀加速下滑 |
B.是为了增大小车下滑的加速度 |
C.可使得橡皮筋做的功等于合力对小车做的功 |
D.可使得橡皮筋松弛后小车做匀速运动 |
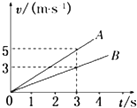
(2)实验中先后用同样的橡皮筋1条、2条、3条……合并起来挂在小车的前端进行多次实验,每次都要把小车拉到同一位置再释放。把第1次只挂1条橡皮筋时橡皮筋对小车做的功记为W1;第二次挂2条橡皮筋时橡皮筋对小车做的功为2W1……橡皮筋对小车做功后而使小车获得的速度可由打点计时器打出的纸带测出。根据第四次实验中打出的纸带(如图所示),可求得小车最终获得的速度为_______m/s。(保留三位有效数字)
![]()
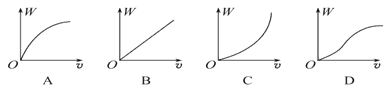
(3)若根据多次测量数据画出的W-v图象如图所示,根据图线形状,可知对W与v的关系符合实际的是图_______。