题目内容
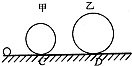在轨道上稳定运行的空间站中，物体处于完全失重状态，有如图所示的装置，半径分别为r和R（R＞r）的甲、乙两个光滑的圆形轨道固定在同一竖直平面上，轨道之间有一条水平轨道CD相通，宇航员让一质量为m小球以初速度v0先滑上甲轨道，通过粗糙的CD段，CD段长度为L，又滑上乙轨道，最后离开两圆轨道，小球经过乙轨道最高点时对轨道的压力为分析：该装置处于稳定运行的空间站中，处于完全失重状态，所以小球对水平轨道的压力为0．在圆轨道中运动，靠轨道的压力提供向心力．小球在完全失重情况下运动，在圆轨道和直轨道上速度的大小都不变．
解答：解：在空间站中的物体处于完全失重状态，小球对水平轨道CD的压力为零，小球经过CD段时不受摩擦力，不需要克服摩擦力做功，在整个过程中小球速度保持不变，在乙轨道的最高点，轨道的弹力提供小球做圆周运的向心力，由牛顿第二定律得：轨道对球的支持力：F=
，由牛顿第三定律得：球对轨道的压力：F′=F=
；
故答案为：
．
m
| ||
| R |
m
| ||
| R |
故答案为：
m
| ||
| R |
点评：解决本题的关键知道小球处于完全失重状态，在直轨道上不受摩擦力，做匀速直线运动，在圆轨道上做匀速圆周运动．
练习册系列答案
相关题目
（2011?上海模拟）在轨道上稳定运行的空间站中，有如图所示的装置，半径分别为r和R（R＞r）的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，轨道之间有一条水平轨道CD相通，宇航员让一小球以一定的速度先滑上甲轨道，通过粗糙的CD段，又滑上乙轨道，最后离开两圆轨道，那么下列说法正确的是（ ）
在轨道上稳定运行的空间站中，有如图所示的装置，半径分别为r和R（R＞r）的甲、乙两个光滑的圆形轨道固定在同一竖直平面上，轨道之间有一条水平轨道CD相通，宇航员让一小球以一定的速度先滑上甲轨道，通过粗糙的CD段，又滑上乙轨道，最后离开两圆轨道，那么下列说法正确的是（ ）