题目内容
7.设地球和火星都在同一平面上绕太阳做匀速圆周运动,火星轨道半径为地球轨道半径的1.5倍.现从地球表面向火星发射火星探测器,发射过程分两步,第一步:在地球表面用火箭对探测器加速,使它脱离地球引力成为一个沿地球轨道运动的“星体”;第二步:在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,从而使探测器沿半个椭圆轨道(该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切,如图1所示)射到火星上.$\sqrt{5}$=2.2,$\sqrt{1.5}$=1.2,1年为365天.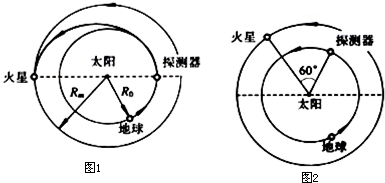
(1)求火星公转的周期为多少天(地球日)?
(2)求火星探测器沿椭圆轨道运动到火星上经历的时间为多少天?
(3)当探测器沿地球轨道稳定运动后,在某年5月1日零时,测得探测器与火星间的角距离为60°,如图2所示,问应在何年何月何日点燃探测器的发动机,才能使探测器正好落在火星上?
分析 (1)根据开普勒第三定律列式即可求解;
(2)探测器和地球都围绕太阳运动,设探测器的周期为t,地球周期为T0.依据开普勒第三定律即可求解;
(3)为使探测器落到火星上,必须选择适当时机点燃探测器上的火箭发动机,使得探测器沿椭圆轨道到达与火星轨道的相切点时,火星也恰好运行到这一点.已知地球的公转周期,根据开普勒第三定律求出火星的周期,根据半长轴的大小求出探测器在椭圆轨道上的周期,抓住探测器、火星转动的角速度关系,结合转动的角距离得出探测器和火星到达同一点经历的天数
解答 解:(1)根据开普勒第三定律得:
$\frac{{{r}_{地}}^{3}}{{{T}_{地}}^{2}}$=$\frac{{{r}_{火}}^{3}}{{{T}_{火}}^{2}}$
因为r火=1.5r地
解得:T火=1.8T地=1.8×365=657天,即火星公转的周期为657天,
(2)探测器和地球都围绕太阳运动,设探测器的周期为t,地球周期为T0.依据开普勒第三定律有:
$\frac{(\frac{{R}_{m}+{R}_{0}}{2})^{3}}{{t}^{2}}=\frac{{{R}_{0}}^{3}}{{{T}_{0}}^{2}}$,解得:t=$\frac{5\sqrt{5}}{8}年$=502天,
探测器的飞行时间${t}_{1}=\frac{t}{2}=251天$
(3))为使探测器沿椭圆轨道到达与火星轨道的相切点时,火星恰好运行到这一点,必须选择适当时机点燃火箭发动机.
地球公转的运动周期Td=365天
地球公转的角速度 ${ω}_{d}=\frac{360°}{365天}=0.968°/天$
火星公转周期Tm=657天
火星公转角速度ωm=$\frac{360°}{657天}$=0.548°/天
探测器从点燃火箭发动机至到达火星所需时间为${t}_{1}=\frac{t}{2}=251天$
探测器运行至火星的251天内,火星运行的角度为θm=ωmt1=0.548°/天×251天=137.5°
为了使探测器到达火星轨道时,正好射到火星上,那么探测器在椭圆轨道近日点点燃火箭发动机时,火星应在其远日点的切点之前137.5°处,即探测器点燃发动机时,与火星的角度应为180°-137.5°=42.5°
但是,已知某年3月1日零时探测器与火星的角距离为 60°(火星在前,探测器在后),为使其角度成为 42.5°,必须等待一段时间,设为t天,使二者达到角距离42.5°的合适位置.t 满足60°-42.5°=(ωd-ωm)$t=\frac{60°-42.5°}{{ω}_{d}-{ω}_{m}}=\frac{17.5}{0.42}=42天$
因此点燃火箭发动机的时刻应为当年的 3月1日之后42天,即同年的 4月11日.
答:(1)火星公转的周期为657天;
(2)火星探测器的飞行时间为251天;
(3)应在同年的 4月11日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面.
点评 本题主要考查了开普勒第三定律的应用,知道为使探测器落到火星上,必须选择适当时机点燃探测器上的火箭发动机,使得探测器沿椭圆轨道到达与火星轨道的相切点时,火星也恰好运行到这一点,难度较大.

| A. | 线速度 | B. | 角速度 | C. | 加速度 | D. | 向心力 |
| A. | 小船渡江的轨迹为曲线 | |
| B. | 小船到达离江岸边$\frac{d}{2}$处,船渡江的速度为$\sqrt{5}$v0 | |
| C. | 小船渡江时的轨迹为直线 | |
| D. | 小船到达离南江岸$\frac{3d}{4}$处,船渡江的速度为$\sqrt{10}$v0 |
| A. | 真空中上述雷达发射的电磁波的波长范围在0.3m至1.5m之间 | |
| B. | 电磁波是由恒定不变的电场或磁场产生的 | |
| C. | 测出从发射电磁波到接收反射波的时间间隔可以确定雷达和目标的距离 | |
| D. | 波长越短的电磁波,越不容易发生衍射 |
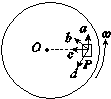 如图所示,物块P置于水平转盘上随转盘一起运动,且与圆盘相对静止,图中c沿半径指向圆心,a与c垂直,下列说法正确的是( )
如图所示,物块P置于水平转盘上随转盘一起运动,且与圆盘相对静止,图中c沿半径指向圆心,a与c垂直,下列说法正确的是( )| A. | 当转盘匀速转动时,P受摩擦力方向为c方向 | |
| B. | 当转盘加速转动时,P受摩擦力方向可能为b方向 | |
| C. | 当转盘加速转动时,P受摩擦力方向可能为a方向 | |
| D. | 当转盘减速转动时,P受摩擦力方向可能为d方向 |
| A. | 4倍 | B. | 8倍 | C. | 16倍 | D. | 64倍 |