Question

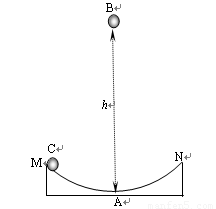
C如图所示，光滑的弧形槽的半径为R（R远大于弧长MN），A为弧形槽的最低点．小球B放在A点正上方，离A点的高度为h，小球C放在M点．同时释放两球，使两球正好在A点相碰，则从建立模型的角度分析，小球C的运动可视为

单摆

模型，h应为

1

8

π2(2n+1)2R（n=0，1，2…）

．

Answer 1

分析：小球的运动可视为单摆模型，抓住小球C的运动时间和小球B的时间相等，通过单摆的周期公式求出C球经过最低点的时间，从而根据自由落体运动的位移公式求出高度h．

解答：解：小球C的运动可以视为单摆的模型，摆长等于圆弧的半径．
小球自由落体运动的时间t，有：h=

1

2

gt2
摆球C的周期为：T=2π

R g

则有：t=(2n+1)

T

4

联立解得：h=

1

8

π2(2n+1)2R（n=0，1，2…）．
故答案为：单摆；

1

8

π2(2n+1)2R （n=0，1，2…）

点评：解决本题的关键抓住时间相等，通过单摆的周期公式进行求解，注意C球运动的周期性．