题目内容
 如图所示,-个上表面水平的劈形物体A放在倾角为θ固定的光滑斜面上,在其上表面放一个光滑小球B,两物体的质量均为m,让劈形物体从静止开始释放,则在小球碰到斜面之前的运动过程中,下列说法正确的有
如图所示,-个上表面水平的劈形物体A放在倾角为θ固定的光滑斜面上,在其上表面放一个光滑小球B,两物体的质量均为m,让劈形物体从静止开始释放,则在小球碰到斜面之前的运动过程中,下列说法正确的有
- A.B的运动轨迹是沿斜面向下的直线
- B.B的运动轨迹是竖直向下的直线
- C.A、B的位移大小之比为1:sinθ
- D.A、B的加速度大小之比为1:tanθ
BC
分析:分析小球m的受力情况,根据牛顿第一定律分析小球在水平方向和竖直方向的运动状态,即可确定其运动轨迹.
根据几何关系确定A、B的位移关系,再由运动学公式求解加速度之比.
解答:A、B楔形物体A释放前,小球受到重力和支持力,两力平衡;楔形物体A释放后,由于小球是光滑的,则小球水平方向不受力,根据牛顿第一定律知道,小球在水平方向的状态不改变,即仍保持静止状态.而竖直方向:楔形物体A对B的支持力将小于小球的重力,小球将沿竖直方向做加速运动,所以小球在碰到斜面前的运动是竖直向下的加速运动,其运动轨迹是竖直向下的直线,故A错误,故B正确.
C、根据几何关系可知:A、B的位移大小之比为xA:xB=1:sinθ.故C正确.
D、由运动学公式x= ,t相等,则知A、B的加速度大小之比为1:sinθ.故D错误.
,t相等,则知A、B的加速度大小之比为1:sinθ.故D错误.
故选BC
点评:本题关键要正确分析小球的受力情况,抓住水平方向不受力,状态不发生改变是关键.同时要根据几何知识求解位移之比,从而加速度之比.
分析:分析小球m的受力情况,根据牛顿第一定律分析小球在水平方向和竖直方向的运动状态,即可确定其运动轨迹.
根据几何关系确定A、B的位移关系,再由运动学公式求解加速度之比.
解答:A、B楔形物体A释放前,小球受到重力和支持力,两力平衡;楔形物体A释放后,由于小球是光滑的,则小球水平方向不受力,根据牛顿第一定律知道,小球在水平方向的状态不改变,即仍保持静止状态.而竖直方向:楔形物体A对B的支持力将小于小球的重力,小球将沿竖直方向做加速运动,所以小球在碰到斜面前的运动是竖直向下的加速运动,其运动轨迹是竖直向下的直线,故A错误,故B正确.
C、根据几何关系可知:A、B的位移大小之比为xA:xB=1:sinθ.故C正确.
D、由运动学公式x=
 ,t相等,则知A、B的加速度大小之比为1:sinθ.故D错误.
,t相等,则知A、B的加速度大小之比为1:sinθ.故D错误.故选BC
点评:本题关键要正确分析小球的受力情况,抓住水平方向不受力,状态不发生改变是关键.同时要根据几何知识求解位移之比,从而加速度之比.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
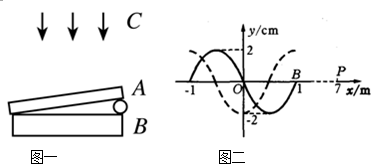
 如图所示为两个单摆做受迫振动中的共振曲线,则下列说法正确的是( )
如图所示为两个单摆做受迫振动中的共振曲线,则下列说法正确的是( )| A、两个单摆的固有周期之比为TⅠ:TⅡ=2:5 | B、若两个受迫振动是在地球上同一地点进行,则两个摆长之比为lⅠ:lⅡ=4:25 | C、图线Ⅱ若是在地球表面上完成的,则该摆摆长约为1 m | D、若两个受迫振动分别在月球上和地球上进行,且摆长相等,则图线Ⅱ是月球上的单摆的共振曲线 |
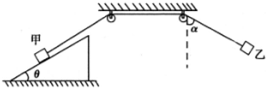 如图所示的装置中.表面粗糙的斜面固定在地面上.斜面的倾角为θ=30°两个光滑的定滑轮的半径很小,用一根跨过定滑轮的细线连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内摆动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1kg,若重力加速度g取10m/s2.下列说法不正确的是( )
如图所示的装置中.表面粗糙的斜面固定在地面上.斜面的倾角为θ=30°两个光滑的定滑轮的半径很小,用一根跨过定滑轮的细线连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内摆动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1kg,若重力加速度g取10m/s2.下列说法不正确的是( )