题目内容
【题目】如图所示，A、B、C三个物体放在旋转圆台上，它们与圆台之间的动摩擦因数均为μ，A的质量为2m，B、C质量均为m，A、B离轴心距离为R，C离轴心2R，则当圆台旋转时（设A、B、C都没有滑动）
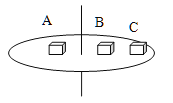
A. 物体C的向心加速度最大
B. 物体B受到的静摩擦力最大
C. ω=
是C开始滑动的临界角速度
D. 当圆台转速增加时，B比A先滑动
【答案】AC
【解析】A、物体绕轴做匀速圆周运动，角速度相等，有
，由于C物体的转动半径最大，故加速度最大，故A正确；
B、物体绕轴做匀速圆周运动，角速度相等，静摩擦力提供向心力，根据牛顿第二定律，有： 
，故B的摩擦力最小，故B错误；
C、物体C恰好滑动时，静摩擦力达到最大，有： 
，解得： 
即转动半径最大的最容易滑动，故物体C先滑动，物体A、B一起后滑动，故选项C正确，选项D错误。
练习册系列答案
名校课堂系列答案
相关题目
