题目内容
【题目】如图所示,传送带长6m,与水平方向的夹角37°,以5m/s的恒定速度向上运动.一个质量为2kg的物块(可视为质点),沿平行于传送带方向以10m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,g=10m/s2.求:

(1)物块刚滑上传送带时的加速度大小;
(2)物块到达传送带顶端时的速度大小.
【答案】(1)10m/s2 (2)4m/s
【解析】(1)物块刚滑上传送带时,物块的加速度大小为a1,由牛顿第二定律有:
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=gsin37°+μgcos37°=10×0.6+0.5×10×0.8=10m/s2;
(2)设物块速度减为5m/s所用时间为t1,则v0-v=a1t1
解得:t1=0.5s
通过的位移:x1=![]() ×0.5m=3.75m<6m
×0.5m=3.75m<6m
因μ<tanθ,此后物块继续减速上滑的加速度大小为a2则:mgsin37°-μmgcos37°=ma2
代入数据解得:a2=2m/s2
设物块到达最高点的速度为v1,则:v2-v12=2a2x2
x2=l-x1=2.25m
解得:v1=4m/s.

【题目】某同学探究弹力与弹簧伸长量的关系.
①将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧时,长度记为L0 , 弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6 , 数据如下表表:
代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
表中有一个数值记录不规范,代表符号为 . 由表可知所用刻度尺的最小长度为 .
③图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与的差值(填“L0或L1”).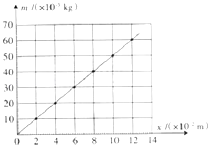
④由图可知弹簧的劲度系数为N/m;通过图和表可知砝码盘的质量为g(结果保留两位有效数字,重力加速度取9.8m/s2).