题目内容
 一质量为500kg的木箱放于质量为2000kg的平板车的后部,木箱到驾驶室的距离L=1.6m,已知木箱与平板车间的动摩擦因数u=0.484,平板车运动过程中所受的阻力是车和箱总重的0.2倍,平板车以Vo=22m/s的恒定速率行驶,突然驾驶员刹车,使车做匀减速运动,为让木箱不撞击驾驶室,g取10,试求:
一质量为500kg的木箱放于质量为2000kg的平板车的后部,木箱到驾驶室的距离L=1.6m,已知木箱与平板车间的动摩擦因数u=0.484,平板车运动过程中所受的阻力是车和箱总重的0.2倍,平板车以Vo=22m/s的恒定速率行驶,突然驾驶员刹车,使车做匀减速运动,为让木箱不撞击驾驶室,g取10,试求:(1)从刹车开始到平板车完全停止至少要经过多长时间?
(2)驾驶员刹车时的制动力不能超过多少?
分析:(1)从刹车开始到平板车完全停止运动过程,平板车和箱子都做匀减速运动,由牛顿第二定律求出箱子的加速度大小.由运动学公示求出车子的加速度大小.为让木箱恰好不撞击驾驶室,箱子与车子的位移之差恰好等于L,联立求解时间t.
(2)对车子进行研究,由牛顿第二定律求解刹车时的制动力.
(2)对车子进行研究,由牛顿第二定律求解刹车时的制动力.
解答:解:(1)从刹车开始到平板车完全停止,至少要经过的时间为t,此时,平板车刹车的加速度大小为a车,木箱的加速度大小为a箱,对木箱,则有:μm木箱g=m木箱a箱
可得:a箱=μg=4.84m/s2,
恰好不相撞时应满足:
-
=L,
又v0=22m/s,L=1.6m,可得a=5m/s2,
那么t═4.4s.
(2)刹车时刻动力最大为F,
则 F-μm木箱g+0.2(m木箱+m车)g=m车a,
可得F=7420N.
答:
(1)从刹车开始到平板车完全停止至少要经过4.4s的时间.
(2)驾驶员刹车时的制动力不能超过7420N.
可得:a箱=μg=4.84m/s2,
恰好不相撞时应满足:
| ||
| 2a箱 |
| ||
| 2a |
又v0=22m/s,L=1.6m,可得a=5m/s2,
那么t═4.4s.
(2)刹车时刻动力最大为F,
则 F-μm木箱g+0.2(m木箱+m车)g=m车a,
可得F=7420N.
答:
(1)从刹车开始到平板车完全停止至少要经过4.4s的时间.
(2)驾驶员刹车时的制动力不能超过7420N.
点评:本题运用牛顿第二定律和运动学结合处理动力学问题,挖掘隐含的临界条件是关键:两者位移之差等于L.

练习册系列答案
相关题目
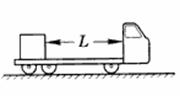
 所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做
所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做 匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求:
匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求: