题目内容
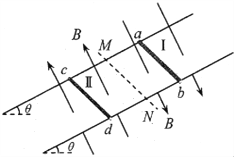
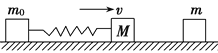
【题目】如图所示,质量分别为M和m0的两滑块用轻弹簧连接,以恒定的速度v沿光滑水平面运动,与位于正对面的质量为m的静止滑块发生碰撞,若碰撞时间极短,则在此碰撞过程中,下列情况不可能发生的是
A. M、m、m0速度均发生变化,分别变为v1、v2、v3,而且满足(M+m0)v=Mv1+mv2+m0v3
B. m0的速度不变,M、m的速度变为v1和v2,且满足Mv=Mv1+mv2
C. m0的速度不变,M和m的速度变为v′,且满足Mv=(M+m)v′
D. M、m、m0速度均发生变化,M和m0速度都变为v1,m的速度变为v2,且满足(M+m0)v=(M+m0)v1+mv2
【答案】BC
【解析】
试题在M和m碰撞的过程中,由于碰撞时间极短,M和m组成的系统动量守恒,m0在瞬间速度不变,应用动量守恒定律分析答题.
解:碰撞的瞬间M和m组成的系统动量守恒,m0的速度在瞬间不变,以M的初速度方向为正方向,若碰后M和m的速度变v1和v2,由动量守恒定律得:
Mv=Mv1+mv2;
若碰后M和m速度相同,由动量守恒定律得:Mv=(M+m)v′.
故BC正确,AD错误.
故选:BC.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目