题目内容
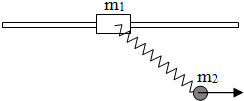 质量为m1的木块套在光滑的水平杆上,轻质弹簧一端系在木块上,另一端系住质量为m2的小球,在水平恒力(大小未知)作用下,m1、m2一起以加速度a在竖直平面内沿水平方向作匀加速直线运动,运动过程中m1、m2相对静止,已知弹簧的原长度为L,劲度系数为k,m1、m2可看成质点,求:
质量为m1的木块套在光滑的水平杆上,轻质弹簧一端系在木块上,另一端系住质量为m2的小球,在水平恒力(大小未知)作用下,m1、m2一起以加速度a在竖直平面内沿水平方向作匀加速直线运动,运动过程中m1、m2相对静止,已知弹簧的原长度为L,劲度系数为k,m1、m2可看成质点,求:(1)运动过程中m1、m2之间的距离;
(2)撤去水平恒力的瞬时m1、m2的加速度.
分析:(1)分别两个物体为研究对象,分析受力情况,根据牛顿第二定律求出弹簧的弹力,由胡克定律可求出弹簧的伸长量,即可求出m1、m2之间的距离.
(2)撤去水平恒力的瞬时弹簧的弹力不变,m1的受力情况不变,加速度不变,m2的合力等于-m1a,即可求出m2的加速度.
(2)撤去水平恒力的瞬时弹簧的弹力不变,m1的受力情况不变,加速度不变,m2的合力等于-m1a,即可求出m2的加速度.
解答:解:(1)设弹簧与水平方向的夹角为α,弹簧的弹力大小为F,
以m1为研究对象,则有 Fcosα=m1a
以m2为研究对象,则有 Fsinα=m2g
则得 F=
故运动过程中m1、m2之间的距离为 S=L+
=L+
(2)撤去水平恒力的瞬时弹簧的弹力不变,m1的受力情况不变,加速度不变,仍为a;
m2的合力大小等于Fcosα=m1a,m2的加速度为a2=
.
答:(1)运动过程中m1、m2之间的距离是L+
;
(2)撤去水平恒力的瞬时m1的加速度为a,m2的加速度为
.
以m1为研究对象,则有 Fcosα=m1a
以m2为研究对象,则有 Fsinα=m2g
则得 F=
| (m1a)2+(m2g)2 |
故运动过程中m1、m2之间的距离为 S=L+
| F |
| k |
| ||
| k |
(2)撤去水平恒力的瞬时弹簧的弹力不变,m1的受力情况不变,加速度不变,仍为a;
m2的合力大小等于Fcosα=m1a,m2的加速度为a2=
| -m1a |
| m2 |
答:(1)运动过程中m1、m2之间的距离是L+
| ||
| k |
(2)撤去水平恒力的瞬时m1的加速度为a,m2的加速度为
| -m1a |
| m2 |
点评:本题采用隔离法研究连接体问题,也可以运用整体法和隔离法结合分析.

练习册系列答案
相关题目

 质量为m1的木块套在光滑的水平杆上,轻质弹簧一端系在木块上,另一端系住质量为m2的小球,在水平恒力(大小未知)作用下,m1、m2一起以加速度a在竖直平面内沿水平方向作匀加速直线运动,运动过程中m1、m2相对静止,已知弹簧的原长度为L,劲度系数为k,m1、m2可看成质点,求:
质量为m1的木块套在光滑的水平杆上,轻质弹簧一端系在木块上,另一端系住质量为m2的小球,在水平恒力(大小未知)作用下,m1、m2一起以加速度a在竖直平面内沿水平方向作匀加速直线运动,运动过程中m1、m2相对静止,已知弹簧的原长度为L,劲度系数为k,m1、m2可看成质点,求:
