题目内容
5.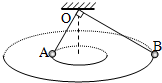 如图所示,两根长度不同的细线OA、OB分别系有两个相同的小球,两细线的上端都系于O点.设法使两个小球在水平面内做匀速圆周运动,其中OAB始终处于同一竖直平面且OA⊥OB,细线长度之比为OA:OB=1:$\sqrt{3}$.则下列关于两小球的运动描述正确的是( )
如图所示,两根长度不同的细线OA、OB分别系有两个相同的小球,两细线的上端都系于O点.设法使两个小球在水平面内做匀速圆周运动,其中OAB始终处于同一竖直平面且OA⊥OB,细线长度之比为OA:OB=1:$\sqrt{3}$.则下列关于两小球的运动描述正确的是( )| A. | A小球的轨道平面高于B小球的轨道平面 | |
| B. | OA、OB两条细线的拉力之比1:$\sqrt{3}$ | |
| C. | A、B两小球的线速度之比为1:3 | |
| D. | A、B两小球的轨道半径之比为1:$\sqrt{3}$ |
分析 小球受重力和拉力,两个力的合力提供小球做圆周运动的向心力,由力的合成法分析拉力大小,由牛顿第二定律列式比较两球的线速度之比,由几何关系分析轨道半径之比.
解答 解:A、由题知,OA:OB=1:$\sqrt{3}$,OA⊥OB,则OAcos30°=OBsin30°,所以两球在同一轨道平面内运动,故A错误.
B、对于任意一球,设绳与竖直方向夹角为θ,O到轨道平面内的高度为h,则细线的拉力 T=$\frac{mg}{cosθ}$,则OA、OB两条细线的拉力之比 TA:TB=$\frac{1}{cos30°}$:$\frac{1}{cos60°}$=1:$\sqrt{3}$,故B正确.
C、由牛顿第二定律得:mgtanθ=m$\frac{{v}^{2}}{R}$,得v=$\sqrt{gRtanθ}$=$\sqrt{g•htanθ•tanθ}$∝tanθ,则A、B两小球的线速度之比为 vA:vB=tan30°:tan60°=1:3,故C正确.
D、A、B两小球的轨道半径之比为 RA:RB=htan30°:htan60°=1:3.故D错误.
故选:BC
点评 解决本题的关键会正确地受力分析,知道匀速圆周运动向心力是由物体所受的合力提供,通过列式进行定量分析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.客运轮船在九江至武汉之间做往返航班运行时刻表上(如下表所示),最右边一列是自九江起的公里数,根据表中数据,估算武汉至九江间长江的平均流速为多少?
| 上行 | 港名 | 下行 | 公里数 | ||
| 到港 | 离岗 | 离岗 | 到港 | ||
| 07:40 | 九江 | 22:00 | 0 | ||
| 10.30 | 武穴 | 20:00 | 19:30 | 50 | |
| 14:30 | 黄石 | 16:40 | 16:10 | 126 | |
| 不靠岸 | 鄂州 | 14:50 | 14:30 | 169 | |
| 21:30 | 武汉 | 11:00 | 269 | ||
20. 如图所示,a为地球赤道上的物体,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球同步卫星.关于a、b、c做匀速圆周运动的说法中正确的是( )
如图所示,a为地球赤道上的物体,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球同步卫星.关于a、b、c做匀速圆周运动的说法中正确的是( )
 如图所示,a为地球赤道上的物体,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球同步卫星.关于a、b、c做匀速圆周运动的说法中正确的是( )
如图所示,a为地球赤道上的物体,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球同步卫星.关于a、b、c做匀速圆周运动的说法中正确的是( )| A. | 地球对a、b、c三星的万有引力提供了其各自的向心力 | |
| B. | 线速度的大小关系为va<vc<vb | |
| C. | 向心加速度的大小关系为aa>ab>ac | |
| D. | 周期关系为Tc>Tb>Ta |
10.如图所示,一木块受到垂直于倾斜墙面方向的推力F作用而处于静止状态,下列判断正确的是( )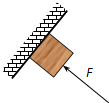

| A. | 墙面与木块间的弹力可能为零 | |
| B. | 墙面对木块的摩擦力方向沿倾斜墙面向上 | |
| C. | 在推力F逐渐增大过程中,木块将始终维持静止状态 | |
| D. | 在推力F逐渐增大过程中,木块所受墙面的摩擦力始终不变 |
17.关于磁场对通电直导线作用力的大小,下列说法中正确的是( )
| A. | 通电直导线跟磁场方向平行时作用力最大 | |
| B. | 通电直导线跟磁场方向垂直时作用力最大 | |
| C. | 通电直导线跟磁场方向有夹角时作用力最大 | |
| D. | 以上说法都不对 |
14.下列说法正确的是( )
| A. | 当研究一列火车全部通过桥所需的时间,因为火车上各点的运动状态相同,所以可以把火车视为质点 | |
| B. | 打点计时器是一种测量长度的仪器 | |
| C. | 位移和路程都是描述质点位置变动的物理量 | |
| D. | (n-1)末就是指第ns初 |
15.如图为一轻质弹簧的长度和弹力的关系图线正确的是( )
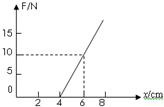

| A. | 弹簧的原长为6cm | |
| B. | 弹簧的劲度系数K=5N/m | |
| C. | 弹簧拉伸5cm时弹力的大小为25N | |
| D. | 随着弹力F的增大,弹簧的劲度系数K也增大 |
 在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=$\frac{2\sqrt{3}}{3}$m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形圆域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=$\frac{2\sqrt{3}}{3}$m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形圆域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求: