题目内容
17. 如图所示,MDN为绝缘材料制成的半径为R的光滑竖直半圆环,置于磁感应强度为B,方向垂直纸面向外的匀强磁场中,一质量为m,电荷量为-q的小球从M点无初速下落,D为圆环最低点,则下列说法中正确的是( )
如图所示,MDN为绝缘材料制成的半径为R的光滑竖直半圆环,置于磁感应强度为B,方向垂直纸面向外的匀强磁场中,一质量为m,电荷量为-q的小球从M点无初速下落,D为圆环最低点,则下列说法中正确的是( )| A. | 小球滑到D点时速率满足V<$\sqrt{2gR}$ | |
| B. | 小球由M滑到D点所用时间与磁场无关 | |
| C. | 小球滑到D点时对圆环轨道的压力一定大于mg | |
| D. | 小球滑到D点时对圆环轨道的压力随圆环半径的增大而增大 |
分析 伦兹力的方向指向圆心,不改变速度的大小,根据动能定理求出到达D点时的速度.根据牛顿第二定律,径向的合力提供向心力,求出轨道对小球的支持力.
解答 解:A、从M点运动到D点的过程中只有重力做功,根据动能定理得:
mgR=$\frac{1}{2}$mv2,
解得:v=$\sqrt{2gR}$.故A错误;
B、因为洛伦兹力始终对小球不做功,故根据动能定理洛伦兹力不改变小球速度的大小,故有无磁场不影响小球的圆周运动的快慢,故B正确;
C、小球运动到D点时若受到的洛伦兹力的方向向上,则有:N+qvB-mg=$\frac{{mv}^{2}}{R}$,
解得:N=3mg-qvB,知不一定大于重力mg,故C错误;
D、由以上的分析:N=3mg-qvB=3mg-qB$\sqrt{2gR}$,知半径增大,支持力减小,则压力减小.故D错误.
故选:B
点评 本题综合运用了动能定理和牛顿第二定律,关键是受力分析,运用合适的规律进行解题.

练习册系列答案
相关题目
12.根据给出的速度和加速度的正负,对下列运动性质的判断不正确的是( )
| A. | v0<0、a<0,物体做加速运动 | |
| B. | v0<0、a>0,物体先做加速运动,后做减速运动 | |
| C. | v0>0、a<0,物体先做减速运动,后做加速运动 | |
| D. | v0>0、a=0,物体做匀减速直线运动 |
2.用一束光照射金属表面,能发生光电效应,若需要增大光电子的最大初动能,应采取的办法是( )
| A. | 增大照射光的强度 | B. | 增大照射光的频率 | ||
| C. | 延长照射的时间 | D. | 增大照射光的波长 |
3.在磁场中,某点磁感应强度的方向应是( )
| A. | 放入该点处的通电直导线所受磁场力的方向 | |
| B. | 放入该点处小磁针S极的受力方向 | |
| C. | 运动的电荷在该点处所受到的洛伦兹力的方向 | |
| D. | 通过该点处磁感线的切线方向 |

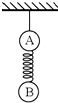 如图所示,A的质量为3m,B的质量为2m,两球用细线悬挂于天花板上静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间,A球加速度为$\frac{5}{3}g$;B球加速度为0.(已知重力加速度为g)
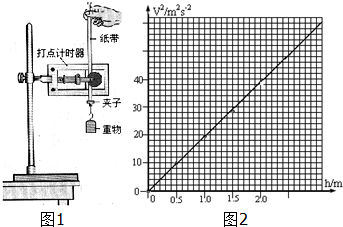
如图所示,A的质量为3m,B的质量为2m,两球用细线悬挂于天花板上静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间,A球加速度为$\frac{5}{3}g$;B球加速度为0.(已知重力加速度为g) 在用DIS实验系统验证牛顿第三定律的实验中,获得了如图所示的图象.
在用DIS实验系统验证牛顿第三定律的实验中,获得了如图所示的图象.