题目内容
甲、乙两个物体都做匀速圆周运动.转动半径比为3:4,在相同的时间里甲转过60圈时,乙转过45圈,则它们所受的向心加速度之比为( )
分析:根据角速度定义ω=
可知甲、乙的角速度之比,再由向心加速度公式a=ω2r可以求出他们的向心加速度之比.
| △θ |
| △t |
解答:解:相同时间里甲转过60圈,乙转过45圈,根据角速度定义ω=
可知
ω1:ω2=4:3
由题意
r1:r2=3:4
根据a=ω2r得:
a1:a2=4:3
故选B
| △θ |
| △t |
ω1:ω2=4:3
由题意
r1:r2=3:4
根据a=ω2r得:
a1:a2=4:3
故选B
点评:要熟悉角速度定义公式和向心加速度公式,能根据题意灵活选择向心加速度公式!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙两个物体分别做匀变速直线运动,甲的加速度为1.0m/s2,乙的加速度为-2.0m/s2,根据这些条件做出的以下判断,其中正确的是( )
| A、乙的加速度大于甲的加速度 | B、甲做的是匀加速运动,乙做的是匀减速运动 | C、两个物体的速度都不可能为零 | D、两个物体的运动方向可能相反 |
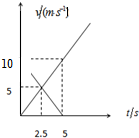 甲乙两个物体都做直线运动,它们的v-t图象如图所示,则以下说法正确的是( )
甲乙两个物体都做直线运动,它们的v-t图象如图所示,则以下说法正确的是( )