题目内容
【题目】如图所示，一个质量为1kg的煤块从光滑曲面上高度H=1.25m处无初速释放，到达底端时水平进入水平传送带，传送带由一电动机驱动着匀速向左转动，速率为3m/s．已知煤块与传送带间的动摩擦因数μ=0.2．煤块冲上传送带后就移走光滑曲面．（g取10m/s2）．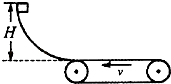
（1）若两皮带轮之间的距离是6m，煤块将从哪一边离开传送带？
（2）若皮带轮间的距离足够大，从煤块滑上到离开传送带的整个过程中，由于煤块和传送带间的摩擦而产生的划痕长度有多长？摩擦力对煤块做的功为多大？
【答案】
（1）解：煤块从曲面上下滑时机械能守恒，有 
解得煤块滑到底端时的速度 
以地面为参照系，煤块滑上传送带后向右做匀减速运动直到速度为零，期间煤块的加速度大小和方向都不变，加速度大小为 
，
煤块从滑上传送带到相对地面速度减小到零，对地向右发生的位移为 
，煤块将从右边离开传送带
答：煤块将从右边离开传送带
（2）解：以地面为参考系，若两皮带轮间的距离足够大，则煤块滑上传送带后向右做匀减速运动直到速度为零，后向左做匀加速运动，直到速度与传送带速度相等后与传送带相对静止，从传送带左端掉下，期间煤块的加速度大小和方向都不变，加速度大小为 ．
取向右为正方向，煤块发生的位移为 
，
煤块运动的时间为 
，
这段时间内皮带向左运动的位移大小为s2=vt=3×4m=12m
煤块相对于传送带滑行的距离为△s=s1+s2=16m，
根据动能定理得， 
= 
答：煤块和传送带间的摩擦而产生的划痕长度为16m，摩擦力对煤块做的功为﹣8J
【解析】（1）根据机械能守恒定律求出煤块到达最低点的速度，根据牛顿第二定律求出煤块在传送带上匀减速直线运动的加速度，结合速度位移公式求出速度减为零的位移，与传送带的长度比较，判断煤块从哪一边离开传送带．（2）物体滑上传送带后向右做匀减速运动直到速度为零，后向左做匀加速运动，直到速度与传送带速度相等后与传送带相对静止，根据运动学公式求出物块的位移大小和传送带的位移大小，从而得出相对位移的大小，结合动能定理求出摩擦力对煤块做功的大小．
【考点精析】解答此题的关键在于理解滑动摩擦力的相关知识，掌握滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解，以及对机械能守恒及其条件的理解，了解在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变．
