题目内容
7.一矿井深80m,在井口每隔一段时间落下一个小球,当第9个小球刚从井口开始下落时,第1个小球恰好到达井底.则(1)相邻两个小球下落的时间间隔是0.5s;
(2)这时第3个小球与井底相距35m.(g取10 m/s2)
分析 根据自由落体运动的位移时间公式求出小球下落的时间,从而得出相邻两个小球下落的时间间隔.结合第3个小球下落的时间求出下落的高度,从而得出与井底的距离.
解答 解:根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×80}{10}}s=4s$,
当第9个小球刚从井口开始下落时,第1个小球恰好到达井底,之间有8个间隔,则相邻两个小球下落的时间间隔$T=\frac{t}{8}s=0.5s$.
由题意知第3个小球下落的时间为t′=3s,
则第3个小球下落的高度$h′=\frac{1}{2}gt{′}^{2}=\frac{1}{2}×10×9m=45m$,距离井底的高度h″=h-h′=80-45m=35m.
故答案为:0.5,35.
点评 解决本题的关键知道自由落体运动的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
18. 若从砖墙前的某高处使一个石子由静止自由落下,用照相机拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹AB.已知该照相机的曝光时间为0.015s,每块砖的平均厚度为7.5cm,这个石子大约是从距离位置A多高处自由落下( )
若从砖墙前的某高处使一个石子由静止自由落下,用照相机拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹AB.已知该照相机的曝光时间为0.015s,每块砖的平均厚度为7.5cm,这个石子大约是从距离位置A多高处自由落下( )
 若从砖墙前的某高处使一个石子由静止自由落下,用照相机拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹AB.已知该照相机的曝光时间为0.015s,每块砖的平均厚度为7.5cm,这个石子大约是从距离位置A多高处自由落下( )
若从砖墙前的某高处使一个石子由静止自由落下,用照相机拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹AB.已知该照相机的曝光时间为0.015s,每块砖的平均厚度为7.5cm,这个石子大约是从距离位置A多高处自由落下( )| A. | 5m | B. | 3m | C. | 1m | D. | 7m |
15.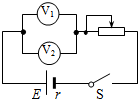 将两个相同的微安表改成量程不同的电压表,再把它们并联接在电路中,开关S闭合后,下列说法正确的是( )
将两个相同的微安表改成量程不同的电压表,再把它们并联接在电路中,开关S闭合后,下列说法正确的是( )
 将两个相同的微安表改成量程不同的电压表,再把它们并联接在电路中,开关S闭合后,下列说法正确的是( )
将两个相同的微安表改成量程不同的电压表,再把它们并联接在电路中,开关S闭合后,下列说法正确的是( )| A. | 两表指针偏转角度相同,示数相同 | B. | 两表指针偏转角度相同,示数不同 | ||
| C. | 两表指针偏转角度不同,示数相同 | D. | 两表指针偏转角度不同,示数不同 |
2.老鼠离开洞穴后沿直线运动.若测得它距洞穴口不同距离s时的速度大小如下表所示.由表中数据可以推知,老鼠的运动速度v与它距洞穴口距离s的关系式为vs=3.老鼠从距洞穴口1m处运动到距洞穴口2m处所用的时间为0.5s.
| s(m) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| v(m/s) | 6.0 | 3.0 | 2.0 | 1.5 | 1.2 | 1.0 |
12.关于速度和加速度,下列说法正确的是( )
| A. | 速度变化越大,加速度就越大 | |
| B. | 加速度方向不变,速度方向也一定保持不变 | |
| C. | 加速度减小,速度也一定减小 | |
| D. | 加速度增大,速度可以减小 |
17.质点做直线运动的位移x与时间t的关系为x=t2+5t(各物理量均采用国际单位),则该质点( )
| A. | 第1s内的位移是5m | B. | 前2s内的平均速度是7m/s | ||
| C. | 第3s初的速度是11m/s | D. | 任意1s内的速度增量都是2m/s |

 如图所示,物体A重力GA=20N,物体B重力GB=40N,A与B、B与地之间的动摩擦系数?相同?用水平绳将物体A系在竖直墙壁上,水平力F向右拉物体B,当F=30N时,刚好能将B匀速拉出?求
如图所示,物体A重力GA=20N,物体B重力GB=40N,A与B、B与地之间的动摩擦系数?相同?用水平绳将物体A系在竖直墙壁上,水平力F向右拉物体B,当F=30N时,刚好能将B匀速拉出?求