题目内容
10. 如图所示,真空中有一块直角三角形的玻璃砖ABC,∠B=30°,若CA的延长线上S点有一点光源发出的一条光线由D点射入玻璃砖,光线经玻璃砖折射后垂直BC边射出,且此光束从S 传播到D的时间与在玻璃砖内的传播时间相等,已知光在真空中的传播速度为c,BD=$\sqrt{2}$d,∠ASD=15°.求:
如图所示,真空中有一块直角三角形的玻璃砖ABC,∠B=30°,若CA的延长线上S点有一点光源发出的一条光线由D点射入玻璃砖,光线经玻璃砖折射后垂直BC边射出,且此光束从S 传播到D的时间与在玻璃砖内的传播时间相等,已知光在真空中的传播速度为c,BD=$\sqrt{2}$d,∠ASD=15°.求:①玻璃砖的折射率;
②SD两点间的距离.
分析 ①由几何关系可求出入射角i和折射角r,再由折射定律求解折射率.
②根据光束经过SD用时和在玻璃砖内的传播时间相等,列式可求得SD两点间的距离.
解答  解:①由几何关系可知入射角i=45°,折射角r=30°,则玻璃砖的折射率为:
解:①由几何关系可知入射角i=45°,折射角r=30°,则玻璃砖的折射率为:
n=$\frac{sini}{sinr}$
可得:n=$\sqrt{2}$
②在玻璃砖中光速为:v=$\frac{c}{n}$
光束经过SD和玻璃砖内的传播时间相等有:$\frac{SD}{c}$=$\frac{BDsin30°}{v}$
又 BD=$\sqrt{2}$d
得:SD=d
答:①玻璃砖的折射率是$\sqrt{2}$;
②SD两点间的距离是d.
点评 解答本题的关键是依据几何关系和折射定律、光速公式解题,解题时要作出光路图.

练习册系列答案
相关题目
20. 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )| A. | A球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为零 | |
| C. | A球到达最低点时的速度为2$\sqrt{\frac{3gL}{5}}$ | |
| D. | 以后A球一定能回到释放点 |
18.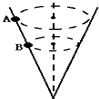 如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
 如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的角速度等于球B的角速度 | |
| B. | 球A的线速度等于球B的线速度 | |
| C. | 球A的向心加速度等于球B的向心加速度 | |
| D. | 球A对内壁的压力大于球B对内壁的压力 |
19.关于第一宇宙速度的说法中正确的是( )
| A. | 第一宇宙速度是发射卫星的最大速度 | |
| B. | 第一宇宙速度的数值是11.2km/s | |
| C. | 第一宇宙速度是近地绕地卫星应具有的速度 | |
| D. | 第一宇宙速度是卫星做圆周运动的最小线速度 |
20. 电阻器、电容器和电感器是电子设备中常用的电子元件.如图所示电路图中,符号“C”表示的元件是( )
电阻器、电容器和电感器是电子设备中常用的电子元件.如图所示电路图中,符号“C”表示的元件是( )
 电阻器、电容器和电感器是电子设备中常用的电子元件.如图所示电路图中,符号“C”表示的元件是( )
电阻器、电容器和电感器是电子设备中常用的电子元件.如图所示电路图中,符号“C”表示的元件是( )| A. | 电阻器 | B. | 电容器 | C. | 电感器 | D. | 电源 |

 2015年第53届世界乒乓球锦标赛在我国苏州举行,中国健儿在比赛中取得了十分优异的成绩,这些成绩的背后是运动员刻苦的训练和顽强的拼搏,如图所示是运动员训练时用的乒乓球发射器示意图,发射口距桌面高度为h=0.45m,假定乒乓球水平射出,落在桌面上与发射口水平距离x=2.4m的P点,飞行过程中未触网,乒乓球质量m=0.0027kg,不计空气阻力,取g=10m/s2,求:
2015年第53届世界乒乓球锦标赛在我国苏州举行,中国健儿在比赛中取得了十分优异的成绩,这些成绩的背后是运动员刻苦的训练和顽强的拼搏,如图所示是运动员训练时用的乒乓球发射器示意图,发射口距桌面高度为h=0.45m,假定乒乓球水平射出,落在桌面上与发射口水平距离x=2.4m的P点,飞行过程中未触网,乒乓球质量m=0.0027kg,不计空气阻力,取g=10m/s2,求: