题目内容
一宇宙探测器从某一星球的表面竖直升空，假设探测器的质量为1500kg，发动机的推力为恒力，宇宙探测器升空到某一高度时，发动机突然关闭，如图表示其速度随时间的变化规律．求：（1）探测器在该行星表面达到的最大高度；
（2）计算探测器在加速上升过程中的加速度；
（3）计算该行星表面的重力加速度（假设行星表面没有空气阻力）
分析：在速度-时间图象中，某一点代表此时刻的瞬时速度，时间轴上方速度是正数，时间轴下方速度是负数；切线代表该位置的加速度，向右上方倾斜，加速度为正，向右下方倾斜加速度为负；图象与坐标轴围成面积代表位移，时间轴上方位移为正，时间轴下方位移为负．
解答：解（1）由图可知，空间探测器在 t1=8 s时具有最大瞬时速度，t2=24 s时才达到最大高度，且其最大高度为图象中△OAB的面积，
hm=768m
（2）空间探测器前8 s内在推动力和星球重力作用下加速上升，
加速上升阶段加速度：a1=
=5m/s2
（3）8 s后只在星球重力作用下减速上升和加速回落．
该行星表面的重力加速度为：g=
=-2.5m/s2
答：（1）探测器在该行星表面达到的最大高度768m；
（2）计算探测器在加速上升过程中的加速度5m/s2；
（3）计算该行星表面的重力加速度2.5m/s2．
hm=768m
（2）空间探测器前8 s内在推动力和星球重力作用下加速上升，
加速上升阶段加速度：a1=
| △v |
| △t |
（3）8 s后只在星球重力作用下减速上升和加速回落．
该行星表面的重力加速度为：g=
| △v |
| △t |
答：（1）探测器在该行星表面达到的最大高度768m；
（2）计算探测器在加速上升过程中的加速度5m/s2；
（3）计算该行星表面的重力加速度2.5m/s2．
点评：本题是为速度--时间图象的应用，要明确斜率的含义，知道在速度--时间图象中图象与坐标轴围成的面积的含义，能根据图象读取有用信息结合牛顿第二定律解题．
练习册系列答案
阅读快车系列答案
相关题目
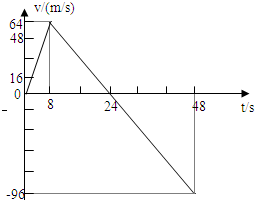
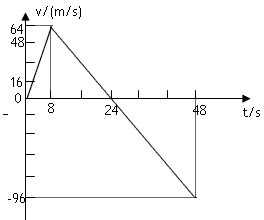
一宇宙探测器从某一星球的表面竖直升空，假设探测器的质量为1500kg，发动机的推力为恒力，宇宙探测器升空到某一高度时，发动机突然关闭，如图表示其速度随时间的变化规律．求：
一宇宙探测器从某一星球的表面竖直升空，假设探测器的质量为1500kg，发动机的推力为恒力，宇宙探测器升空到某一高度时，发动机突然关闭，如图表示其速度随时间的变化规律．求：