题目内容
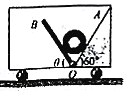
【题目】电子质量为m、电荷量为q，以速度v0与x轴成θ角射入磁感应强度为B的匀强磁场中，最后落在x轴上的P点，如图所示，求：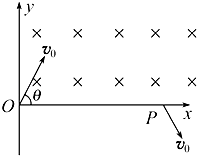
（1）OP的长度；
（2）电子从由O点射入到落在P点所需的时间t．
【答案】
（1）
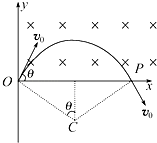
解：过O点和P点作速度方向的垂线，两线交点C即为电子在磁场中做匀速圆周运动的圆心，电子运动轨迹如图所示
电子在磁场中做匀速圆周运动，洛伦兹力提供向心力，
由牛顿第二定律得：qv0B=m 
，
解得电子轨道半径：R= 
，
由几何知识得：OP=2Rsinθ= 
sinθ
（2）
解：由图示可知，电子做圆周运动转过的圆心角：φ=2θ，
电子做圆周运动的周期：T= 
，
电子在磁场中运动的时间：t= 
T= 
× = 
【解析】（1）电子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律可以求出电子的轨道半径，然后由几何知识求出OP间的距离．（2）由几何知识求出电子在磁场中转过的圆心角，然后求出电子在磁场中的运动时间．
【考点精析】本题主要考查了向心力的相关知识点，需要掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力才能正确解答此题．
练习册系列答案
相关题目
