题目内容
2.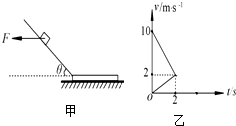 如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,木板与水平面间的摩擦因素为0.1.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平面上前2s运动的v-t图象如图乙所示,g=10m/s2.求
如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,木板与水平面间的摩擦因素为0.1.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平面上前2s运动的v-t图象如图乙所示,g=10m/s2.求(1)水平作用力F的大小;
(2)滑块静止在斜面上的位置离木板上表面的高度h;
(3)木板的质量;
(4)木板在水平面上移动的距离.
分析 (1)对滑块受力分析,由共点力的平衡条件可得出水平作用力的大小;
(2)根据图乙判断滑块滑到斜面底部的速度,由牛顿第二定律求出加速度,从而根据在斜面上的位移和三角关系求出下滑时的高度.
(3)根据摩擦力的公式求出地面和木板间的摩擦力,根据牛顿第二定律求出滑块和木板间的摩擦力,进而根据牛顿第二定律求出木板的质量;
(4)根据v-t图中的面积求出速度相等前木板的位移;由牛顿第二定律求出木板与滑块一起做减速运动的加速度,然后求出木板减速运动的位移,求和即可.
解答 解:(1)滑块受到水平推力F、重力mg和支持力N处于平衡,如图所示,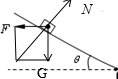
水平推力:F=mgtanθ=1×10×$\frac{\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}N$
(2)由图乙知,滑块滑到木板上时速度为:v1=10m/s
设下滑的加速度为a,由牛顿第二定律得:mgsinθ+Fcosθ=ma
代入数据得:a=10m/s2
则下滑时的高度:h=$\frac{{{v}_{1}}^{2}}{2a}•sinθ=\frac{100}{20}•\frac{1}{2}=2.5m$
(3)设在整个过程中,地面对木板的摩擦力为f,滑块与木板间的摩擦力为f1
由图乙知,滑块刚滑上木板时加速度为:${a}_{1}=\frac{△v}{△t}=\frac{2-10}{2-0}=-4m/{s}^{2}$
对滑块:f1=ma1 ①
此时木板的加速度:${a}_{2}=\frac{△v}{△t}=\frac{2-0}{2-0}=1m/{s}^{2}$
对木板:-f1-f=Ma2 ②
当滑块和木板速度相等后连在一起做匀减速直线运动,受到的摩擦力:f=μ•(M+m)g ③
联立①②③带入数据解得:M=1.5kg
(4)木板加速过程中的位移:${x}_{1}=\frac{0+v}{2}•{t}_{1}=\frac{0+2}{2}×2=2$m
当滑块和木板速度相等后连在一起做匀减速直线运动,由牛顿第二定律:
(M+m)a3=f
代入数据得:${a}_{3}=1m/{s}^{2}$
所以木板减速阶段的位移:${x}_{2}=\frac{0-{v}^{2}}{-2{a}_{3}}=\frac{0-{2}^{2}}{-2×1}=2$m
木板的总位移:x=x1+x2=2+2=4m
答:(1)水平作用力F的大小位$\frac{10\sqrt{3}}{3}N$;
(2)滑块开始下滑时的高度为2.5m;
(3)木板的质量为1.5kg;
(4)木板在水平面上移动的距离是4m.
点评 本题考查斜面上力的合成与分解,和牛顿第二定律的应用,注意平时深入分析各种运动形式的特征.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案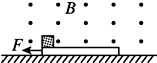 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做加速度减小的变加速运动,最后做速度为10 m/s的匀速运动 | |
| C. | 木板先做加速度为2m/s2的匀加速运动,再做加速度增大的运动,最后做加速度为3 m/s2的匀加速运动 | |
| D. | t=3s后滑块和木板有相对运动 |
 如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m.当无人机悬停在距离地面高度H=180m时,由于动力设备故障,无人机突然失去全部升力,从静止开始竖直坠落,经5s后无人机瞬间又恢复最大升力.g取10m/s2.求:
如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m.当无人机悬停在距离地面高度H=180m时,由于动力设备故障,无人机突然失去全部升力,从静止开始竖直坠落,经5s后无人机瞬间又恢复最大升力.g取10m/s2.求:
 第22届冬季奥林匹克运动会于2014年02月07日~02月23日在俄罗斯联邦索契市举行,中国选手徐梦桃获得自由式滑雪女子空中技巧银牌.假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角为θ=37°的坡顶A由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示.不计空气阻力,坡长为L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
第22届冬季奥林匹克运动会于2014年02月07日~02月23日在俄罗斯联邦索契市举行,中国选手徐梦桃获得自由式滑雪女子空中技巧银牌.假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角为θ=37°的坡顶A由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示.不计空气阻力,坡长为L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: