题目内容
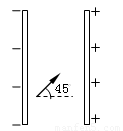
如图所示,某一质量为m的金属滑块,带电量大小为q,以某一速度沿水平放置的木板进入电磁场空 间,匀强磁场的方向垂直纸面向外,电场方向水平向右,滑块与木板之间的摩擦系数为μ.已知滑块由P点沿木板做匀速直线运动到Q点与开关碰撞,将Q点的开关撞开,使电场消失,只保留磁场,离开开关时滑块的动能变为原来的
间,匀强磁场的方向垂直纸面向外,电场方向水平向右,滑块与木板之间的摩擦系数为μ.已知滑块由P点沿木板做匀速直线运动到Q点与开关碰撞,将Q点的开关撞开,使电场消失,只保留磁场,离开开关时滑块的动能变为原来的
,并匀速返回P处,设往复运动的总时为T,P、Q间距离为L,碰撞时间不计.求:
(1)磁感应强度B的大小;
(2)整个过程中克服摩擦力所做的功;
(3)匀强电场E的大小.
 间,匀强磁场的方向垂直纸面向外,电场方向水平向右,滑块与木板之间的摩擦系数为μ.已知滑块由P点沿木板做匀速直线运动到Q点与开关碰撞,将Q点的开关撞开,使电场消失,只保留磁场,离开开关时滑块的动能变为原来的
间,匀强磁场的方向垂直纸面向外,电场方向水平向右,滑块与木板之间的摩擦系数为μ.已知滑块由P点沿木板做匀速直线运动到Q点与开关碰撞,将Q点的开关撞开,使电场消失,只保留磁场,离开开关时滑块的动能变为原来的| 1 | 4 |
(1)磁感应强度B的大小;
(2)整个过程中克服摩擦力所做的功;
(3)匀强电场E的大小.
分析:(1)带正电的小物块在复合场中做匀速直线运动,受到的合力为0,先根据匀速直线它的规律求得小物块的速度;小物块从Q返回P的过程中,小物块在磁场受到的洛伦兹力和重力大小相等,方向相反时,不受摩擦力的作用,才能够做匀速直线运动;然后结合受力求得磁场的磁感应强度;
(2)根据受力求得摩擦力,然后根据W=FS求得摩擦力的功;
(3)根据小物块在复合场中做匀速直线运动,受到的合力为0,求得电场强度.
(2)根据受力求得摩擦力,然后根据W=FS求得摩擦力的功;
(3)根据小物块在复合场中做匀速直线运动,受到的合力为0,求得电场强度.
解答:解:(1)设开始时的速度为V0,则滑块从P-Q-P的过程,有
+
=T
解得:v0=
对滑块从Q-P的过程,进行受力分析知:q(
)B=mg
所以:B=
=
(2)经分析,只有从P-Q的过程,滑块受摩擦力.对滑块从P-Q的过程进行受力分析知:
f=μN=μ(qv0B+mg)=3μmg
摩擦力做功:W=f?L=3μmgL
(3)因物体做匀速运动,得:qE=f
所以:E=
答:(1)磁感应强度B的大小为
;
(2)整个过程中克服摩擦力所做的功为3μmgL;
(3)匀强电场的大小为E=
.
| L |
| v0 |
| L | ||
|
解得:v0=
| 3L |
| T |
对滑块从Q-P的过程,进行受力分析知:q(
| v0 |
| 2 |
所以:B=
| 2mg |
| qv0 |
| 2mgT |
| 3qL |
(2)经分析,只有从P-Q的过程,滑块受摩擦力.对滑块从P-Q的过程进行受力分析知:
f=μN=μ(qv0B+mg)=3μmg
摩擦力做功:W=f?L=3μmgL
(3)因物体做匀速运动,得:qE=f
所以:E=
| 3μmg |
| q |
答:(1)磁感应强度B的大小为
| 2mgT |
| 3qL |
(2)整个过程中克服摩擦力所做的功为3μmgL;
(3)匀强电场的大小为E=
| 3μmg |
| q |
点评:本题是带电物体在复合场中运动的问题,解题的关键是对小物块做出正确的受力分析,找出各个力之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)在光电效应的实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压的关系曲线,如图所示.下列判断正确的是
(1)在光电效应的实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压的关系曲线,如图所示.下列判断正确的是