题目内容
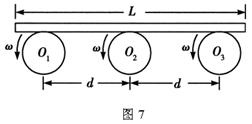
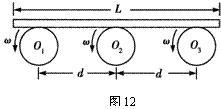
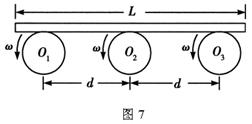
如图7所示,轮子的半径均为R=0.20 m,且均由电动机驱动以角速度ω=8.0 rad/s逆时针匀速转动,轮子的转动轴在同一水平面上,轴心相距d=1.6 m。现将一块均匀木板轻轻地平放在轮子上,开始时木板的重心恰好在O2轮的正上方,已知木板的长度L>2d,木板与轮子间的动摩擦因数均为μ=0.16,则木板的重心恰好运动到O1轮正上方所需要的时间是( )
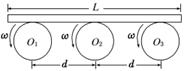
图7
A.1 s B.0.5 s
C.1.5 s D.条件不足,无法判断
解析:选C 轮子边缘点的线速度大小为v=ωR=1.6 m/s,初速度为0的木板放到轮子上后,所受的滑动摩擦力向左,设木板的加速度大小为a,由牛顿第二定律得μmg=ma,a=μg=1.6 m/s2。设木板向左发生位移x时速度达到v,由v2-0=2ax得,x=0.8 m。显然,x<d,故木板先做匀加速运动,后做匀速运动。设加速时间为t1,匀速运动的时间为t2,据x=![]() t1及d-x=vt2可求得t1、t2。所求时间t=t1+t2,解得t=1.5 s,故选C。
t1及d-x=vt2可求得t1、t2。所求时间t=t1+t2,解得t=1.5 s,故选C。

练习册系列答案
相关题目
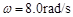 逆时针匀速转动,轮子的转动轴在同一水平面上,轴心相距d=1.6m,现将一块均匀木板轻轻地平放在轮子上,开始时木板的重心恰好在
逆时针匀速转动,轮子的转动轴在同一水平面上,轴心相距d=1.6m,现将一块均匀木板轻轻地平放在轮子上,开始时木板的重心恰好在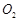 轮的正上方,已知木板的长度L>2d,木板与轮子间的动摩擦因数均为
轮的正上方,已知木板的长度L>2d,木板与轮子间的动摩擦因数均为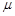 =0.16,则木板的重心恰好运动到
=0.16,则木板的重心恰好运动到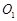 轮正上方所需的时间是( )
轮正上方所需的时间是( )