题目内容
如图所示，某力F，大小等于10 N保持不变，作用在半径r＝1 m的转盘的边缘上，方向任何时刻均沿过作用点的切线方向，则在转盘转动一周的过程中，力F所做的功为
[ ]
A．0 J
B．10 J
C．20πJ
D．无法确定
答案：C
解析：
解析：
|
解析：由于力F的方向总与该时刻的速度方向一致，因此做功不为零，为求力F所做的功，可把作用点所在的圆周分成无限多很短的小段如Δs1、Δs2、Δs3……来研究．对每一足够小的小段来说，力F的方向与该小段的位移方向一致，可用公式W＝Fs求功，则圆盘在力F作用下转动一周的过程中，力F所做的功为： W＝FΔs1＋FΔs2＋FΔs3＋……＝F(Δs1＋Δs2＋Δs3＋……)＝F·2πr＝10×2π×1 J＝20πJ． 选项C正确． 方法归纳 本题采用无限分割再求其和的思维方法求特殊情况下变力的功，体现了高等数学中的“微积分”思想． 研究某个力做功时，若力大小不变而方向改变时，不能简单地看初、末状态而直接用功的定义求功，要具体问题具体分析，因为功描述力对物体持续作用在空间的积累效应，是一个过程量，研究功不能只简单地看初、末状态，而应该研究整个过程． |
练习册系列答案
相关题目
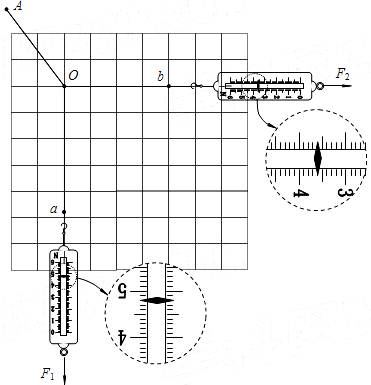
某研究性小组的同学们在探究安培力的大小和方向与哪些因素有关时，设计了以下两个实验．
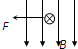
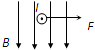
如图所示，某空间存在着垂直纸面向里的匀强磁，A、B两个物块叠放在一起，并置于光滑的绝缘水平面上，物块A带正电，物块B为不带电的绝缘体．水平恒力F作用在物块B上，使A、B一起由静止开始向左运动．在运动过程中，A、B始终保持相对静止，以下关于A、B受力的说法中正确的是（ ）
