题目内容
函数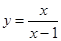 的图像与函数
的图像与函数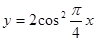
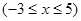 的图像所有交点的纵坐标之和等于( )k.
的图像所有交点的纵坐标之和等于( )k.
A. | B.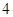 | C. | D. |
B
解析试题分析:先确定函数的对称性,再确定交点的个数,即可得到结论.
因为函数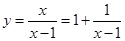 关于
关于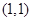 对称,函数
对称,函数 关于
关于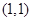 对称,如图所示:两函数有4个交点.
对称,如图所示:两函数有4个交点.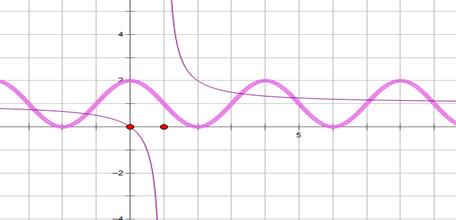
考点:三角函数的图像与性质、余弦函数的图象、函数的对称性、函数的交点问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
在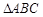 中,若
中,若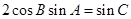 ,则
,则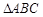 的形状是
的形状是
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
给出下列四个命题,其中错误的命题是( )
①若 ,则
,则 是等边三角形
是等边三角形
②若 ,则
,则 是直角三角形;
是直角三角形;
③若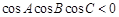 ,则
,则 是钝角三角形;
是钝角三角形;
④若 ,则
,则 是等腰三角形;
是等腰三角形;
| A.①② | B.③④ | C.①③ | D.②④ |
函数 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
将函数 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数 的图象,若
的图象,若 的图象都经过点
的图象都经过点 ,则
,则 的值可以是( )
的值可以是( )
A. | B. | C. | D. |
已知函数 的最小正周期为
的最小正周期为 ,且满足
,且满足 ,则 ( )
,则 ( )
A.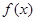 在 在 上单调递减 上单调递减 | B.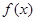 在 在 上单调递减 上单调递减 |
C.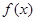 在 在 上单调递增 上单调递增 | D.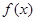 在 在 上单调递增 上单调递增 |
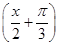 的图象,需将函数y=sin
的图象,需将函数y=sin 的图象至少向左平移( )个单位.
的图象至少向左平移( )个单位.



 的最小正周期是( )
的最小正周期是( )


