题目内容
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
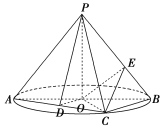
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明AC⊥DO,PO⊥AC,再证明AC⊥平面PDO;(2)当CO⊥AB时,C到AB的距离最大,且最大值为1,再求三棱锥P-ABC体积的最大值;(3)先证明PB=PC=BC,在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,当O,E,C′共线时,CE+OE取得最小值.再求其最小值.
(1)证明:在△AOC中,因为OA=OC,D为AC的中点,所以AC⊥DO.
又PO垂直于圆O所在的平面,所以PO⊥AC.
因为DO∩PO=O,所以AC⊥平面PDO.
(2)解:因为点C在圆O上,所以当CO⊥AB时,C到AB的距离最大,且最大值为1.
又AB=2,所以△ABC面积的最大值为![]() .
.
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为![]() .
.
(3)解:
在△POB中,PO=OB=1,∠POB=90°,
所以![]() .
.
同理![]() ,所以PB=PC=BC.
,所以PB=PC=BC.
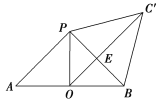
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示.
当O,E,C′共线时,CE+OE取得最小值.
又因为OP=OB,![]() ,所以
,所以![]() 垂直平分PB,即E为PB的中点.
垂直平分PB,即E为PB的中点.
从而![]() ,
,
即CE+OE的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目