题目内容
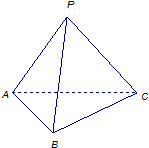 已知边长为
已知边长为| 2 |
(1)求直线PA与BC所成的角;
(2)若M为线段BC上的动点,当BM:BC为何值时,平面PAC与平面PAM所成的锐二面角为45°.
分析:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,转化为向量
与
的夹角求解,注意与直线所成角的关系;
(2)设BM:BC=λ:1(0≤λ<1),则
=λ
=(-λ,λ,0)),
=
+
=(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),可求平面PAM的一个法向量,易知平面PAC的一个法向量为
=(1,0,0),
由题意知,|cos<
,
>|=
,利用向量夹角公式可得关于λ的方程,解出即可;
| PA |
| BC |
(2)设BM:BC=λ:1(0≤λ<1),则
| BM |
| BC |
| AM |
| AB |
| BM |
| m |
由题意知,|cos<
| n |
| m |
| ||
| 2 |
解答: 解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,
解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,
则P(0,0,1),A((0,-1,0),B(1,0,0),C(0,1,0),
=(0,-1,-1),
=(-1,1,0),
cos<
,
>=
=
=-
,
所以<
,
>=120°,直线PA与BC所成的角为60°;
(2)设BM:BC=λ:1(0≤λ<1),则
=λ
=(-λ,λ,0),
=
+
=(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),
设
=(x,y,z)为平面PAM的一个法向量,则
⊥
,
⊥
,
所以
,即
,取
=(
,-1,1),
平面PAC的一个法向量为
=(1,0,0),
当平面PAC与平面PAM所成的锐二面角为45°时,有|cos<
,
>|=
,即
=
=
,
解得λ=3-2
,
故当BM:BC为3-2
时,平面PAC与平面PAM所成的锐二面角为45°.
 解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,
解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,则P(0,0,1),A((0,-1,0),B(1,0,0),C(0,1,0),
| PA |
| BC |
cos<
| PA |
| BC |
| ||||
|
|
| -1 | ||||
|
| 1 |
| 2 |
所以<
| PA |
| BC |
(2)设BM:BC=λ:1(0≤λ<1),则
| BM |
| BC |
| AM |
| AB |
| BM |
设
| n |
| n |
| PA |
| n |
| AM |
所以
|
|
| n |
| 1+λ |
| 1-λ |
平面PAC的一个法向量为
| m |
当平面PAC与平面PAM所成的锐二面角为45°时,有|cos<
| n |
| m |
| ||
| 2 |
| ||||
|
|
| ||||
|
| ||
| 2 |
解得λ=3-2
| 2 |
故当BM:BC为3-2
| 2 |
点评:本题考查二面角的平面角及其求法、异面直线所成角,考查空间向量的运算,考查学生的推理论证能力.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
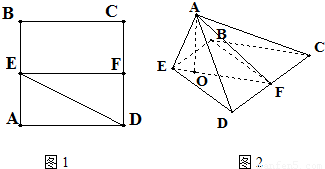
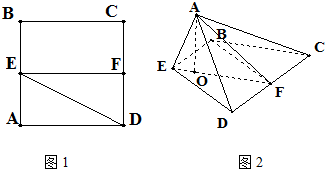 已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.
已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上. (2012•门头沟区一模)已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC上的一点.
(2012•门头沟区一模)已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC上的一点.