题目内容
设P表示幂函数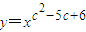 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-2c|>1对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-2c|>1对任意x∈R恒成立的c的集合.(1)求P∩Q;
(2)试写出一个解集为P∩Q的不等式.
【答案】分析:(1)根据幂函数的性质得到幂函数为增函数时,指数大于0,求出解集即可得到P;因为不等式|x-1|+|x-2c|>1对任意x∈R恒成立,即只需找到不等式|x-1|+|x-2c|的最小值即可求出c的范围得到Q,然后求出P∩Q;
(2)根据(1)求出的P∩Q,可以举例为解集为P∩Q的一个不等式即可.
解答:解:(1)∵幂函数 在(0,+∞)上是增函数,∴c2-5c+6>0,即P=(-∞,2)∪(3,+∞),
在(0,+∞)上是增函数,∴c2-5c+6>0,即P=(-∞,2)∪(3,+∞),
又不等式|x-1|+|x-2c|>1对任意x∈R恒成立,∴|2c-1|>1,即Q=(-∞,0)∪(1,+∞),
∴P∩Q=(-∞,0)∪(1,2)∪(3,+∞).
(2)一个解集为P∩Q的不等式可以是 x(x-1)(x-2)(x-3)>0.
点评:考查学生掌握幂函数的增减性,理解函数恒成立时所取的条件,以及会求集合并集的运算.本题第二问是开放性题目,答案不唯一,考查学生发散思维的能力.
(2)根据(1)求出的P∩Q,可以举例为解集为P∩Q的一个不等式即可.
解答:解:(1)∵幂函数
 在(0,+∞)上是增函数,∴c2-5c+6>0,即P=(-∞,2)∪(3,+∞),
在(0,+∞)上是增函数,∴c2-5c+6>0,即P=(-∞,2)∪(3,+∞),又不等式|x-1|+|x-2c|>1对任意x∈R恒成立,∴|2c-1|>1,即Q=(-∞,0)∪(1,+∞),
∴P∩Q=(-∞,0)∪(1,2)∪(3,+∞).
(2)一个解集为P∩Q的不等式可以是 x(x-1)(x-2)(x-3)>0.

点评:考查学生掌握幂函数的增减性,理解函数恒成立时所取的条件,以及会求集合并集的运算.本题第二问是开放性题目,答案不唯一,考查学生发散思维的能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
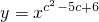 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-2c|>1对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-2c|>1对任意x∈R恒成立的c的集合.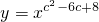 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合. 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合. 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合. 在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合.
在(0,+∞)上是增函数的c的集合;Q表示不等式|x-1|+|x-4|≥c对任意x∈R恒成立的c的集合.