题目内容

在(1-x)5＋(1-x)6＋(1-x)7＋(1-x)8的展开式中，含x3的项的系数是（    ）

A.74             B.121              C.-74                D.-121

思路解析：思路一:先求和,再求系数.

原式=，求含x3的项的系数，等价于求 (1-x)5-(1-x)9中含x4的项的系数，即为=-121.

思路二：逐一求出，然后相加.

(1-x)5,(1-x)6,(1-x)7,(1-x)8中x3的项的系数分别为，-故所求x3的项的系数为=-121.

答案：D

练习册系列答案
相关题目
曲线C的方程是y=x（1≤x≤5），则下列四点中在曲线C上的是（　　）
A、（0，0）
B、（
1
5
，
1
5
）
C、（1，5）
D、（4，4）
在(1+x)5+(1+x)6+(1+x)7的展开式中,x4的系数是通项公式为an=3n-5的数列的(    )

A.第20项             B.第18项             C.第11项              D.第3项

在(1+x)5+(1+x)6+(1+x)7的展开式中,含x4项的系数是等差数列an=3n－5的(　　)

A.第2项               B.第11项             C.第20项             D.第24项

已知函数y=f（x）是定义在区间上的偶函数，且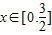时，f（x）=-x2-x+5
（1）求函数f（x）的解析式；
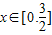（2）将函数g（x）=-x2-x+5，的图象按向量a=（1，b）（b∈R）平移得到函数h（x）的图象，求函数h（x）的解析式并解不等式h（x）＜0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网