Question

直线x=m，y=x将圆面x²+y²≤4分成若干块．现在用5种不同的颜色给这若干块涂色，每块只涂一种颜色，且任意两块不同色，若共有120种不同的涂法，则实数m的取值范围是 ________．

Answer 1

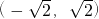
分析：由题意知Y=X与X=m两直线的交点必在Y=X这条直线上，而要想使任意两块不同色共有涂法120种，必须让直线X=m，Y=X将圆分成四块不同的面积，那么不同的涂法是5×4×3×2，要求出Y=X与圆的交点，得到结果．
解答：由题意知Y=X与X=m两直线的交点必在Y=X这条直线上，
而要想使任意两块不同色共有涂法120种，
∴必须让直线X=m，Y=X将圆分成四块不同的面积，
那么不同的涂法才能是5×4×3×2=120．
要求出Y=X与圆的交点分别为（-，-）（，）．
∴-≤m≤，
∵当m=或-时，两直线只能把该圆分成三个区域，
∴不成立，
∴-＜m＜．
故答案为：（-，）
点评：本题考查排列组合问题在解析几何中的应用，在计算时要求做到，兼顾所有的条件，注意实际问题本身的限制条件．