题目内容
已知全集∪={1,2,3,4,5,6}.
(Ⅰ)求集合U的非空子集的个数;
(Ⅱ)若集合M={2,3},集合N满足M⊆N⊆∪,记集合N元素的个数为ξ,求ξ的分布列数数学期望Eξ.
(Ⅰ)求集合U的非空子集的个数;
(Ⅱ)若集合M={2,3},集合N满足M⊆N⊆∪,记集合N元素的个数为ξ,求ξ的分布列数数学期望Eξ.
分析:(Ⅰ)由全集∪={1,2,3,4,5,6},能求出集合U的非空子集的个数.
(Ⅱ)ξ的所有取值为2,3,4,5,6.满足条件的集合N所有可能的结果总数为:
+
+
+
+
=24=16.分别求出每个随机变量ξ的概率,由此能得以ξ的分布列和数学期望.
(Ⅱ)ξ的所有取值为2,3,4,5,6.满足条件的集合N所有可能的结果总数为:
| C | 0 4 |
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
| C | 4 4 |
解答:(本小题满分13分)
解:(Ⅰ)∵全集∪={1,2,3,4,5,6},
∴集合U的非空子集的个数为26-1=63个.…(5分)
(Ⅱ)ξ的所有取值为2,3,4,5,6.
满足条件的集合N所有可能的结果总数为:
+
+
+
+
=24=16.…(7分)
则每个随机变量ξ的概率分别为:
P(ξ=2)=
=
,
P(ξ=3)=
=
,
P(ξ=4)=
=
,
P(ξ=5)=
=
,
P(ξ=6)=
=
.…(11分)
所以ξ的分布列为:
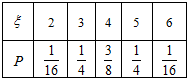
Eξ=2×
+3×
+4×
+5×
+6×
=4.…(13分)
解:(Ⅰ)∵全集∪={1,2,3,4,5,6},
∴集合U的非空子集的个数为26-1=63个.…(5分)
(Ⅱ)ξ的所有取值为2,3,4,5,6.
满足条件的集合N所有可能的结果总数为:
| C | 0 4 |
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
| C | 4 4 |
则每个随机变量ξ的概率分别为:
P(ξ=2)=
| ||
| 16 |
| 1 |
| 16 |
P(ξ=3)=
| ||
| 16 |
| 1 |
| 4 |
P(ξ=4)=
| ||
| 16 |
| 3 |
| 8 |
P(ξ=5)=
| ||
| 16 |
| 1 |
| 4 |
P(ξ=6)=
| ||
| 16 |
| 1 |
| 16 |
所以ξ的分布列为:

Eξ=2×
| 1 |
| 16 |
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 4 |
| 1 |
| 16 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
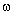 B)∪A;
B)∪A;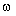 P)。
P)。