题目内容
已知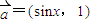 ,
,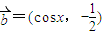 ,函数
,函数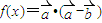 ,那么下列四个命题中正确命题的序号是 .
,那么下列四个命题中正确命题的序号是 .①f(x)是周期函数,其最小正周期为2π.
②当
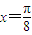 时,f(x)有最小值
时,f(x)有最小值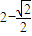 .
.③[-
 π,-
π,- π]是函数f(x)的一个单调递增区间;
π]是函数f(x)的一个单调递增区间;④点(-
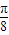 ,2)是函数f(x)的一个对称中心.
,2)是函数f(x)的一个对称中心.
【答案】分析:先化简函数,再一一验证,①f(x)是周期函数,其最小正周期为π;
②当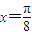 时,
时,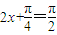 ,所以
,所以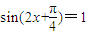 ,可得f(x)有最小值
,可得f(x)有最小值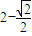 ;
;
③x∈[- π,-
π,- π]时,
π]时,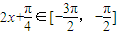 ,可得[-
,可得[- π,-
π,- π]是函数f(x)的一个单调递增区间;
π]是函数f(x)的一个单调递增区间;
④利用(- ,0)是函数g(x)=
,0)是函数g(x)=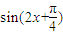 的一个对称中心,可得结论.
的一个对称中心,可得结论.
解答:解:由题意,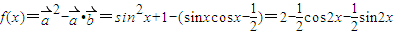 =
=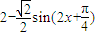 ,∴①f(x)是周期函数,其最小正周期为π,故①错;
,∴①f(x)是周期函数,其最小正周期为π,故①错;
②当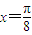 时,
时,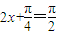 ,∴
,∴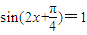 ,∴f(x)有最小值
,∴f(x)有最小值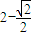 ,故②正确;
,故②正确;
③x∈[- π,-
π,- π]时,
π]时,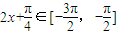 ,∴[-
,∴[- π,-
π,- π]是函数f(x)的一个单调递增区间,故③正确;
π]是函数f(x)的一个单调递增区间,故③正确;
④∵(-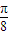 ,0)是函数g(x)=
,0)是函数g(x)=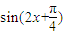 的一个对称中心,∴点(-
的一个对称中心,∴点(-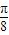 ,2)是函数f(x)的一个对称中心,故④正确
,2)是函数f(x)的一个对称中心,故④正确
故答案为:②③④
点评:本题考查向量知识的运用,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.
②当
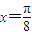 时,
时,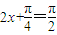 ,所以
,所以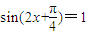 ,可得f(x)有最小值
,可得f(x)有最小值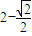 ;
;③x∈[-
 π,-
π,- π]时,
π]时,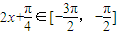 ,可得[-
,可得[- π,-
π,- π]是函数f(x)的一个单调递增区间;
π]是函数f(x)的一个单调递增区间;④利用(-
 ,0)是函数g(x)=
,0)是函数g(x)=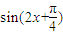 的一个对称中心,可得结论.
的一个对称中心,可得结论.解答:解:由题意,
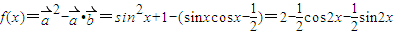 =
=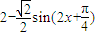 ,∴①f(x)是周期函数,其最小正周期为π,故①错;
,∴①f(x)是周期函数,其最小正周期为π,故①错;②当
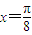 时,
时,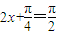 ,∴
,∴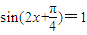 ,∴f(x)有最小值
,∴f(x)有最小值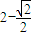 ,故②正确;
,故②正确;③x∈[-
 π,-
π,- π]时,
π]时,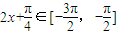 ,∴[-
,∴[- π,-
π,- π]是函数f(x)的一个单调递增区间,故③正确;
π]是函数f(x)的一个单调递增区间,故③正确;④∵(-
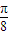 ,0)是函数g(x)=
,0)是函数g(x)=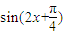 的一个对称中心,∴点(-
的一个对称中心,∴点(-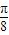 ,2)是函数f(x)的一个对称中心,故④正确
,2)是函数f(x)的一个对称中心,故④正确故答案为:②③④
点评:本题考查向量知识的运用,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目