题目内容
若函数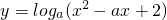 在区间(-∞,1]上为减函数,则a的取值范围是
在区间(-∞,1]上为减函数,则a的取值范围是
- A.(0,1)
- B.[2,+∞)
- C.[2,3)
- D.(1,3)
C
分析:先确定a>1,再转化为t=x2-ax+2在区间(-∞,1]上为减函数,且t>0,即可求得a的取值范围.
解答:若0<a<1,则函数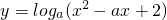 在区间(-∞,1]上为增函数,不符合题意;
在区间(-∞,1]上为增函数,不符合题意;
若a>1,则t=x2-ax+2在区间(-∞,1]上为减函数,且t>0
∴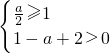 ,2≤a<3
,2≤a<3
即a的取值范围是[2,3)
故选C.
点评:本题考查函数的单调性,考查对数函数,考查学生分析转化问题的能力,属于中档题.
分析:先确定a>1,再转化为t=x2-ax+2在区间(-∞,1]上为减函数,且t>0,即可求得a的取值范围.
解答:若0<a<1,则函数
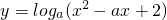 在区间(-∞,1]上为增函数,不符合题意;
在区间(-∞,1]上为增函数,不符合题意;若a>1,则t=x2-ax+2在区间(-∞,1]上为减函数,且t>0
∴
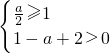 ,2≤a<3
,2≤a<3即a的取值范围是[2,3)
故选C.
点评:本题考查函数的单调性,考查对数函数,考查学生分析转化问题的能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
